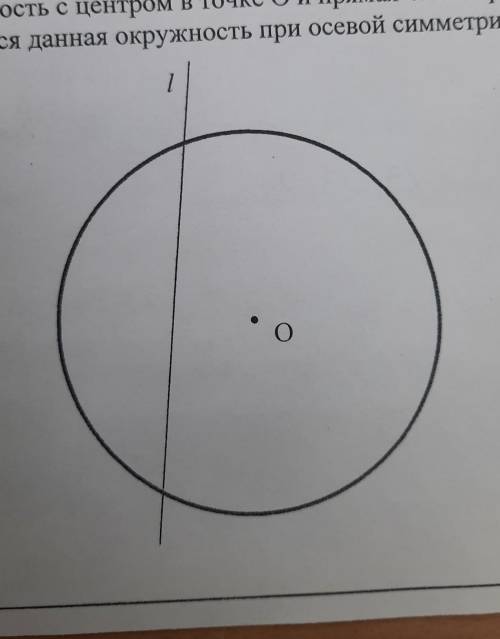
Дана окружность с центром в точке О и прямая l. Построить фигуру F, на которою отображается данная окружность при осевой симметрии с осью l.
​

Для построения фигуры F, которая получается при осевой симметрии данной окружности с осью l, следует выполнить следующие шаги:

1. Определить точку пересечения окружности с прямой l. Пусть эта точка называется A. Чтобы найти эту точку, построим перпендикуляр к прямой l из центра окружности O. Пусть точка пересечения перпендикуляра с прямой l называется B. Соединим точки O и B. Поскольку радиус окружности равен отрезку OB, то радиус можно перенести из точки O на прямую l.

2. Отразить точку O относительно прямой l. Соединим точки O и A линией, а затем проведем перпендикулярную линию к линии OA из точки A. Пусть перпендикуляр пересекает прямую l в точке C.

3. Соединим точки A и C линией. Теперь у нас есть треугольник OAC, который является искомой фигурой F.

Обоснование:
Конструкция основывается на определении осевой симметрии и свойствах перпендикуляров и радиусов окружности.

Осевая симметрия означает, что для каждой точки A, отраженной относительно прямой l, найдется точка B такая, что B находится на той же длине от l, что и A, но с другой стороны.
В данном случае, мы строим отражение центра окружности O по отношению к прямой l и соединяем его с точкой пересечения окружности и прямой A. Таким образом, точка C является отражением точки O относительно линии l.

Треугольник OAC является искомой фигурой F, так как он получается в результате осевой симметрии окружности относительно прямой l. В простых терминах, фигура F является зеркальным отражением окружности относительно линии l.

Этот метод построения фигуры F позволяет наглядно продемонстрировать детям, что осевая симметрия - это отражение фигуры относительно прямой, сохраняющее расстояния между точками.