Дан треугольник ABC, в котором ∠C=90°, а sinB = (4√3):(10√5). Найди cos в квадрате B.

Ответы

Dmitry0232141 20.09.2021 10:40

$\boxed{\ cos^{2} \angle B = \dfrac{113}{125}}$

Объяснение:

Так как угол ∠B является углом прямоугольного треугольника, то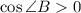 $\cos \angle B 0$ . По основному тригонометрическому тождеству:

$\sin^{2} \angle B + \cos^{2} \angle B = 1$

$\cos^{2} \angle B = 1 - \sin^{2} \angle B = 1 - (\frac{4\sqrt{3} }{10\sqrt{5} })^{2} = 1 - \dfrac{16 * 3}{100 * 5} = 1 - \dfrac{12}{125} = \dfrac{125 - 12}{125}=$

$= \dfrac{113}{125}$ .

Дан треугольник ABC, в котором ∠C=90°, а sinB = (4√3):(10√5). Найди cos в квадрате B.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

kalinkamalinka369 09.09.2019 11:42

Как из 5 таких деталей сделать звезду?...

Вапрос86 09.09.2019 13:10

Впрямоугольном треугольнике авс катеты ас и ав равны.найдите отношение площадей вписанного описанного кругов....

Soniasizova 09.09.2019 13:10

Средняя линия трапеции 9см, одно из ее оснований меньше второго на 6см. найдите большее основание трапеции...

AgentDaleCoop 03.05.2021 14:22

Сторона вписанного в круг правого шестиугольника равна 12 см. Найдите площадь квадрата, нарисованного за пределами этого круга пзлста...

aselznala2004 03.05.2021 14:18

Верно ли то что : радиус описанной около треугольника окружности лежит на пересечении его биссектрис...

pantehnik77777oz07f1 14.06.2019 11:30

1). диагонали прямоугольника abcdпересекается в точке о, abo = 36°. найдите aod. 2). найдите углы прямоугольной трапеции, если один из ее углов равен 20°. 3). стороны параллелограмма...

Александра280306 14.06.2019 11:30

Плоскость альфа проходит через основание ad трапеции abcd точки m и n середины боковых сторон трапеции. докажите что m и n параллельны альфа. найдите a и d, если b и c=4см,...

Аминочка123 14.06.2019 11:20

Прямые а и в пересекаются. прямые а и с параллельны. могут ли прямые в и с быть скрешивающимися? почему, распишите подробно...

Сетора11 14.06.2019 11:20

Прямые mn и ed не лежат в одной плоскости. лежат ли в одной плоскости прямые me и nd...

10203040502017 14.06.2019 11:20

Висота правильноі піраміди 12 см.,а апофема-15 см.обчислити площу поверхні піраміди...

Дан треугольник ABC, в котором ∠C=90°, а sinB = (4√3):(10√5). Найди cos в квадрате B.

Популярные вопросы