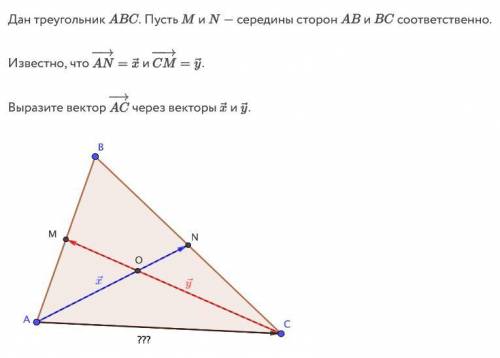
Дан треугольник ABC. Пусть M и N - середины сторон AB и BC соответственно. Известно, что вектор AN = вектор x и вектор CM = вектор y. Выразите вектор AC через векторы x и y.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1)какова масса серебра обьемом 25 см 3серобро обьемом 70 см3 иммеет массу 735...
2 - Как красиво начать сочинение золотая осень....
3 - Вчетырёхугольнике авсd ав||сd? ac=20см, bd=10см, fd=13см. диагонали abcd пересекаются...
1 - 1опишите как происходит развитие живого организма. 2 какие факторы могут остановить...
2 - 8целых 4/7 : 2 целых 22/49 , можно объяснить как делятся дроби?...
3 - Учебник 6 класса просвещение (зеленый, на обложке написаны всякие там синтаксисы,...
1 - Кинозал вмещает 500 зрителей.подсчитай,сколько может быть продано билетов,номера...
3 - Составьте и запишите предложение с данными словами манера, монархия, маникюр,...
2 - Втреугольнике авс угол с равен 30 , ад-биссектриса , угол адв равен 50 найти...
1 - Профессии, существующие в рамках науки !...
1
Пусть векторы x и y имеют вид:
x = (x1, x2)
y = (y1, y2)
Так как N - середина стороны AB, то отрезок AN можно представить в виде суммы векторов AM и MN.
AN = AM + MN
Аналогично, так как M - середина стороны BC, то отрезок CM можно представить в виде разности векторов CB и BM.
CM = CB - BM
Вспомним, что BM = AM, так как точка M является серединой отрезка AB.
BM = AM
Теперь мы можем записать векторы AN и CM, используя выражения AM и BM:
AN = AM + MN = BM + MN = AM + MN
CM = CB - BM = CB - AM
Для решения задачи нам нужно выразить вектор AC через векторы x и y. Для этого мы можем использовать свойство суммирования векторов.
AC = AN + NC = (AM + MN) + (CB - AM)
Теперь мы можем раскрыть скобки и сгруппировать подобные элементы:
AC = AM + MN + CB - AM
Замечаем, что AM и -AM сокращаются:
AC = CB + MN
Осталось выразить вектор MN через векторы x и y. Для этого вспомним, что M и N - середины соответствующих сторон:
MN = (1/2) * BC = (1/2) * (CB - CA)
Подставляем это выражение в формулу для вектора AC:
AC = CB + MN = CB + (1/2) * (CB - CA) = (3/2) * CB - (1/2) * CA
Таким образом, вектор AC выражается через векторы x и y следующим образом:
AC = (3/2) * CB - (1/2) * CA