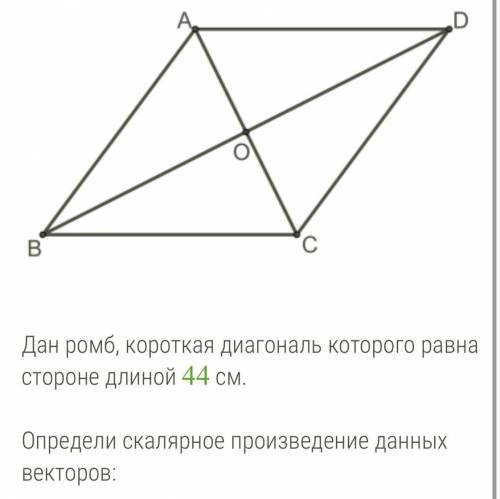
Дан ромб, короткая диагональ которого равна стороне длиной 44 см.

Определи скалярное произведение данных векторов:

1. −→−⋅−→−= ;

2. −→−⋅−→−= ;

3. −→−⋅−→−=

Для того чтобы решить эту задачу, нам необходимо знать, что такое скалярное произведение векторов и как его вычислить.

Скалярное произведение двух векторов определяется следующей формулой:
−→−⋅−→−= |−→−| ⋅ |−→−| ⋅ cos(α), где |−→−| - длина вектора, а α - угол между векторами.

Теперь перейдем к решению задачи step-by-step:

1. Нам дан ромб, в котором короткая диагональ равна стороне длиной 44 см. На рисунке видно, что диагонали ромба делят его на четыре равных треугольника.

2. Мы видим, что длина одной стороны ромба равна 44 см.

3. Так как ромбы являются параллелограммами, то сторона ромба является диагональю прямоугольника, а также является гипотенузой прямоугольного треугольника.

4. В прямоугольном треугольнике можно применить теорему Пифагора для нахождения длины его сторон. Одна из сторон равна 44 см, а другие две стороны будут равными, так как треугольник равнобедренный.

5. Пусть каждая из равных сторон имеет длину х см. Тогда, по теореме Пифагора:
х^2 + х^2 = 44^2.

6. Решив это уравнение, мы найдем значение х. Поэтому, х^2 + х^2 = 44^2 преобразуется к 2x^2 = 1936.

7. Для решения этого уравнения, нам нужно найти квадратный корень из 1936/2. Получаем: x = √(1936/2) = √(968) ≈ 31.089.

8. Таким образом, длина каждой из равных сторон треугольника, а также сторона ромба, равна примерно 31.089 см.

Теперь, когда мы знаем длину стороны ромба, мы можем рассчитать скалярное произведение векторов:

1. −→−⋅−→−= |−→−| ⋅ |−→−| ⋅ cos(α).
−→−⋅−→−= 31.089 ⋅ 44 ⋅ cos(α).

2. Чтобы рассчитать скалярное произведение векторов, нам нужно знать угол α между векторами. Однако, на данном рисунке мы не видим угол. Если предположить, что векторы пересекаются под прямым углом, то угол α будет 90 градусов.

3. Подставляем значения в формулу: −→−⋅−→−= 31.089 ⋅ 44 ⋅ cos(90).
−→−⋅−→−= 31.089 ⋅ 44 ⋅ 0 = 0.

Таким образом, скалярное произведение данных векторов равно 0.

В случае, если угол α между векторами отличается от 90 градусов, мы должны использовать значение cos(α), чтобы рассчитать скалярное произведение. В этом случае, полученный ответ будет отличным от 0.