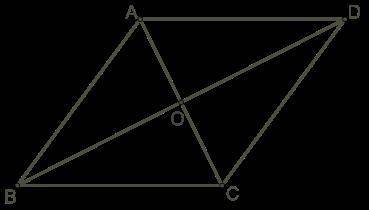
Дан ромб, короткая диагональ которого равна стороне длиной 20 см. Определи скалярное произведение данных векторов:

1. AB−→−⋅AD−→−=
;
2. OB−→−⋅OC−→−=
;
3. BA−→−⋅BC−→−=

Чтобы решить эту задачу, нам нужно знать определение скалярного произведения векторов. Скалярное произведение двух векторов вычисляется как произведение модулей этих векторов и косинуса угла между ними.

1. Для первого вопроса, нам даны векторы AB→ и AD→, и нас просят найти их скалярное произведение (AB−→−⋅AD−→−).

Сначала найдем модули этих векторов:
|AB→| = длина стороны ромба = 20 см
|AD→| = длина диагонали ромба = 20 см

Затем найдем косинус угла между этими векторами. Обратите внимание, что в ромбе угол между АB→ и AD→ составляет 90 градусов (поскольку диагональ ромба делит его на два равнобедренных треугольника). Косинус 90 градусов равен 0.

Теперь можем вычислить скалярное произведение:
AB−→−⋅AD−→− = |AB→| * |AD→| * cos(угол между AB→ и AD→) = 20 см * 20 см * 0 = 0

Ответ: скалярное произведение AB−→ и AD−→ равно 0.

2. Для второго вопроса, нам даны векторы OB→ и OC→, и нас просят найти их скалярное произведение (OB−→−⋅OC−→−).

Аналогично предыдущему шагу, найдем модули этих векторов:
|OB→| = длина стороны ромба = 20 см
|OC→| = длина стороны ромба = 20 см

Косинус угла между OB→ и OC→ также равен 0, поскольку эти векторы сонаправлены (они находятся на одной прямой).

Теперь можем вычислить скалярное произведение:
OB−→−⋅OC−→− = |OB→| * |OC→| * cos(угол между OB→ и OC→) = 20 см * 20 см * 0 = 0

Ответ: скалярное произведение OB−→ и OC−→ равно 0.

3. Для третьего вопроса, нам даны векторы BA→ и BC→, и нас просят найти их скалярное произведение (BA−→−⋅BC−→−).

Теперь будем использовать другой метод для нахождения скалярного произведения. Векторы BA−→ и BC−→ образуют угол 90 градусов (поскольку они лежат на сторонах ромба, которые перпендикулярны друг другу).

Скалярное произведение равно произведению модулей векторов, если угол между ними равен 90 градусов. Таким образом:
BA−→−⋅BC−→− = |BA→| * |BC→| = 20 см * 20 см = 400 см² (поскольку это площадь ромба)

Ответ: скалярное произведение BA−→ и BC−→ равно 400 см².

Таким образом, мы найдем скалярное произведение данных векторов:
1. AB−→−⋅AD−→−= 0
2. OB−→−⋅OC−→−= 0
3. BA−→−⋅BC−→−= 400 см²