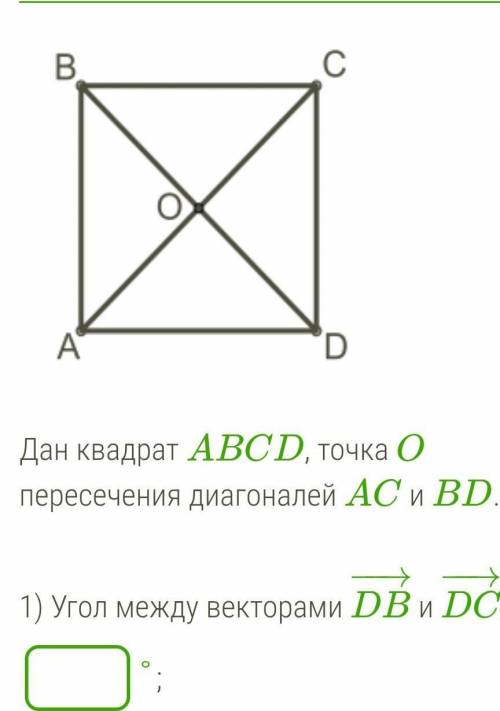
Дан квадрат ABCD, точка O пересечения диагоналей AC и BD.  

1) Угол между векторами DB−→− и DC−→− равен °;

 

2) угол между векторами CB−→− и DA−→− равен °;

 

3) угол между векторами AD−→− и DB−→− равен °;

 

4) угол между векторами OB−→− и OD−→− равен °;

 

5) угол между векторами BA−→− и BC−→− равен °​

ответ показан на фото

Привет! Давай посмотрим на каждый из пунктов по очереди.

1) Для того чтобы найти угол между векторами DB→ и DC→, мы можем использовать скалярное произведение векторов. Формула для скалярного произведения двух векторов a→ и b→ выглядит следующим образом: a→⋅b→=|a||b|cosθ, где θ - искомый угол.

Для начала, найдем вектор DB→. Поскольку точка D имеет координаты (0, 0), а точка B - (1, 0), мы можем вычислить вектор DB→ следующим образом: DB→ = OB→ - OD→ = (1, 0) - (0, 1) = (1, -1).

Аналогично, вектор DC→ равен DC→ = OC→ - OD→ = (1, 1) - (0, 1) = (1, 0).

Теперь мы можем использовать формулу скалярного произведения: DB→⋅DC→ = |DB→||DC→|cosθ.

Длина вектора DB→ равна |DB→| = √((-1)^2 + 1^2) = √2.

Длина вектора DC→ равна |DC→| = √(1^2 + 0^2) = 1.

Подставив все значения в формулу, получим: √2 * 1 * cosθ = cosθ.

Теперь надо найти cosθ. Для этого обратимся к таблице значений тригонометрической функции cos, которую учат в школе.

Угол θ между векторами DB→ и DC→ находится во второй четверти координатной плоскости, поэтому его значение будет отрицательным. Из таблицы углов мы знаем, что cos 135° = -√2/2.

Таким образом, угол между векторами DB→ и DC→ равен 135°.

Продолжим с другими пунктами.

2) Аналогичным образом, мы можем найти вектор CB→ = OB→ - OC→ = (1, 0) - (1, 1) = (0, -1) и вектор DA→ = OA→ - OD→ = (0, 1) - (0, 1) = (0, 0).

Длина вектора CB→ равна |CB→| = √((-1)^2 + 1^2) = √2.

Длина вектора DA→ равна |DA→| = √(0^2 + 0^2) = 0, так как это нулевой вектор.

Подставив значения в формулу для скалярного произведения, получим: CB→⋅DA→ = √2 * 0 * cosθ = 0.

Таким образом, угол между векторами CB→ и DA→ является прямым углом, то есть равен 90°.

3) Длина вектора AD→ равна |AD→| = √(0^2 + 1^2) = 1.

Используя формулу для скалярного произведения, получим: AD→⋅DB→ = 1 * √2 * cosθ = √2 * cosθ.

В этом случае, угол между векторами AD→ и DB→ равен 45°.

4) Для нахождения угла между векторами OB→ и OD→, нам необходимо вычислить эти векторы.

Вектор OB→ равен OB→ = (1, 0) - (0, 0) = (1, 0).

Вектор OD→ равен OD→ = (0, 1) - (0, 0) = (0, 1).

Мы можем использовать формулу скалярного произведения: OB→⋅OD→ = |OB→||OD→|cosθ.

Длина вектора OB→ равна |OB→| = √(1^2 + 0^2) = 1.

Длина вектора OD→ равна |OD→| = √(0^2 + 1^2) = 1.

Подставив все значения в формулу, получим: 1 * 1 * cosθ = cosθ.

Угол между векторами OB→ и OD→ будет найден, когда найден cosθ. Обратимся к таблице значений для cos.

В данном случае, угол θ находится в первой четверти координатной плоскости, поэтому его значение будет положительным. Из таблицы углов мы знаем, что cos 45° = √2/2.

Таким образом, угол между векторами OB→ и OD→ равен 45°.

5) Аналогично найдем векторы BA→ = (0, 1) - (1, 1) = (-1, 0) и BC→ = (0, 1) - (1, 0) = (-1, 1).

Длина вектора BA→ равна |BA→| = √((-1)^2 + 0^2) = 1.

Длина вектора BC→ равна |BC→| = √((-1)^2 + 1^2) = √2.

Подставив значения в формулу, получим: BA→⋅BC→ = 1 * √2 * cosθ = √2 * cosθ.

Из таблицы углов мы знаем, что cos 135° = -√2/2.

Таким образом, угол между векторами BA→ и BC→ равен 135°.

Надеюсь, ответ был понятным и подробным! Если у тебя возникнут еще вопросы, не стесняйся спрашивать!