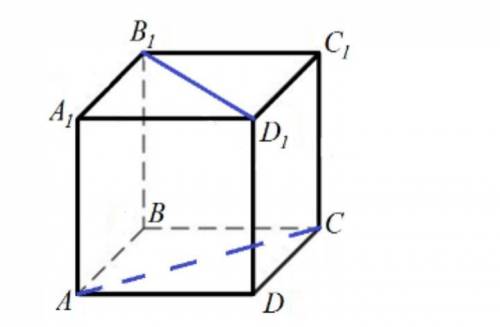
Дан куб ABCDA1B1C1D. Найдите отрезки, перпендикулярные плоскости AA1C1 1) AC1; 2) ВD1; 3) ВD; 4) AA1

Привет! Нет проблем, я с удовольствием помогу тебе разобраться в этой задаче.

Перед тем, как начать, давай уясним, что означает "перпендикулярные плоскости". Две плоскости называются перпендикулярными, если они пересекаются под прямым углом. В данной задаче нам нужно найти отрезки, которые перпендикулярны плоскости AA1C1.

1) Давай найдем отрезок, перпендикулярный плоскости AA1C1 и лежащий на плоскости AC1. Для этого нам понадобятся точки B и D1. Вспомним, что прямые, лежащие на одной плоскости, перпендикулярны к нормали этой плоскости. Найдем нормаль к плоскости AA1C1. Она проходит через точку A и перпендикулярна к плоскости AA1C1. Вектор нормали можно получить путем нахождения векторного произведения двух векторов, лежащих на плоскости AA1C1. Вектором, лежащим на плоскости AA1C1, является вектор AB. Векторным произведением векторов AB и AC1 найдем вектор нормали N:
N = AB x AC1

Теперь у нас есть вектор нормали к плоскости AA1C1. Чтобы найти отрезок, перпендикулярный плоскости и лежащий на плоскости AC1, нам нужно взять какую-то точку этой плоскости, например, C1, и проложить от нее отрезок, параллельный вектору N. Таким образом, искомый отрезок будет равен C1 + t * N, где t - некоторый параметр.

2) Теперь посмотрим на отрезок, перпендикулярный плоскости AA1C1 и лежащий на плоскости BD1. Здесь мы можем использовать тот же самый метод, что и в предыдущем пункте, только вектором нормали будет являться вектор BD1 x BB1.

3) Аналогично, чтобы найти отрезок, перпендикулярный плоскости AA1C1 и лежащий на плоскости BD, мы можем использовать вектор BD x BC.

4) И наконец, чтобы найти отрезок, перпендикулярный плоскости AA1C1 и лежащий на плоскости AA1, мы можем использовать вектор AA1 x A1B.

Все эти вычисления можно проделать с помощью векторных операций, например, векторное произведение и сложение векторов. Я не приведу здесь конкретные численные значения, так как это займет много места, но надеюсь, что объяснение было понятным. Пожалуйста, дай знать, если у тебя есть еще вопросы!