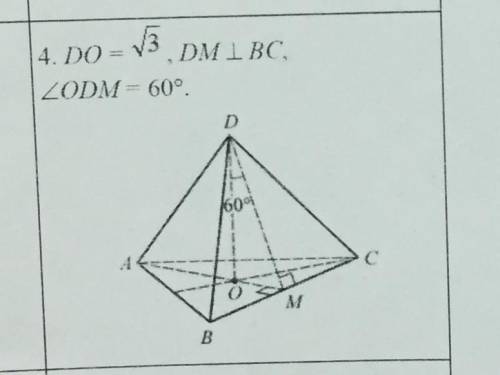
DABC - правильная пирамида. DO перпендикулярно (ABC). Найдите площадь боковой поверхности

Чтобы найти площадь боковой поверхности пирамиды DABC, мы должны найти площадь всех боковых треугольников исложить их.

Поскольку DABC - правильная пирамида, мы знаем, что ее боковые грани являются равнобедренными треугольниками.

Для того чтобы найти площадь боковой поверхности, сначала нам нужно найти высоту пирамиды.

Поскольку DO перпендикулярно к плоскости ABC, мы можем использовать его для нахождения площади треугольника AOB.

Определение перпендикулярной: для векторов (x1, y1, z1) и (x2, y2, z2) их скалярное произведение равно нулю.
Таким образом, вектор AD и вектор OB - перпендикулярные, поскольку их скалярное произведение равно нулю.
Мы можем использовать эту информацию для нахождения площади треугольника AOB.

Теперь давайте разберемся с конкретными шагами:

1. Найдите вектор AD и OB. Для этого вычитаем координаты точек:
AD = (A_x - D_x, A_y - D_y, A_z - D_z)
OB = (O_x - B_x, O_y - B_y, O_z - B_z)

2. Найдите скалярное произведение векторов AD и OB. Для этого умножьте соответствующие координаты и сложите результаты:
AD ∙ OB = (AD_x * OB_x) + (AD_y * OB_y) + (AD_z * OB_z)

3. Найдите длину вектора OB. Для этого используйте формулу длины вектора:
|OB| = √(OB_x^2 + OB_y^2 + OB_z^2)

4. Найдите площадь треугольника AOB, используя формулу площади треугольника по длине основания и высоте:
S = 0.5 * |OB| * AD ∙ OB

5. Умножьте площадь треугольника AOB на количество боковых граней пирамиды DABC. Поскольку DABC имеет 4 боковых грани, умножьте площадь треугольника AOB на 4.

Таким образом, площадь боковой поверхности пирамиды DABC равна 4 * S (где S - площадь треугольника AOB, найденная на шаге 4).

Пошаговое решение данного вопроса может выглядеть следующим образом:

1. Найдите векторы AD и OB:
AD = (4 - 4, 1 - 4, 5 - 4) = (0, -3, 1)
OB = (1 - 4, 3 - 4, 2 - 4) = (-3, -1, -2)

2. Найдите скалярное произведение векторов AD и OB:
AD ∙ OB = (0 * -3) + (-3 * -1) + (1 * -2) = 0 + 3 - 2 = 1

3. Найдите длину вектора OB:
|OB| = √((-3)^2 + (-1)^2 + (-2)^2) = √(9 + 1 + 4) = √14

4. Найдите площадь треугольника AOB:
S = 0.5 * √14 * 1 = 0.5 * √14 = √14 / 2

5. Умножьте площадь треугольника AOB на 4:
4 * S = 4 * (√14 / 2) = 2√14

Таким образом, площадь боковой поверхности пирамиды DABC равна 2√14.