Cos в квадрате 2x + cos в квадрате 6x=1, принадлежащие отрезку [0; Пи/4]
Другие вопросы по теме Геометрия
Популярные вопросы
- Task 8. Choose the wrong part 1. This picture (A) costs (B) five millions...
2 - Проверочная работа на тему Покрытосеменные растения Вариант 21. Семенной...
3 - 4. Сокіл сапсан масою 600 г літає зі швидкістю 320 км/год. Яка його...
3 - Приведите пример «диалога культур» в современном российском обществе?...
1 - Точки А(2;-1;3),С(1;-3;4),D(0;1;-3)-вершины параллелограмма абсд.Найдите...
1 - 1.Що таке Балет ? 2.Що таке хореографія? 3.Що таке кордебалет? 4.Що...
1 - Как найти логарифмический коэффициент передачи? Как искать фазовый сдвиг?...
3 - Інформатика сторона а першого прямокутника дорівнює 4м...
1 - 7. Перепишіть, розкривши дужки. Визначте розряд за значенням виділеноfo...
3 - 3. ( ів) У який момент часу мотоцикліст наздожене ван-тажний автомобіль?А:...
3
Объяснение:
Отберем корни уравнения, принадлежащие отрезку![[0;\frac{\pi}{4} ]](/tpl/images/1358/5689/59225.png) :
:
так как n-целое число, то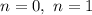
если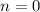 , то
, то 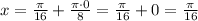
если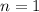 , то
, то 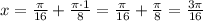
2.
так как n-целое число, то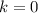
если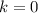 , то
, то 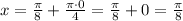
=========================