Через точку , которая находится между параллельными плоскостями α и β, проведены прямые и , пересекающие плоскости так, что точки и находятся в плоскости α,
а точки и — в плоскости β.

= 15 см, = 27 см и =3⋅.

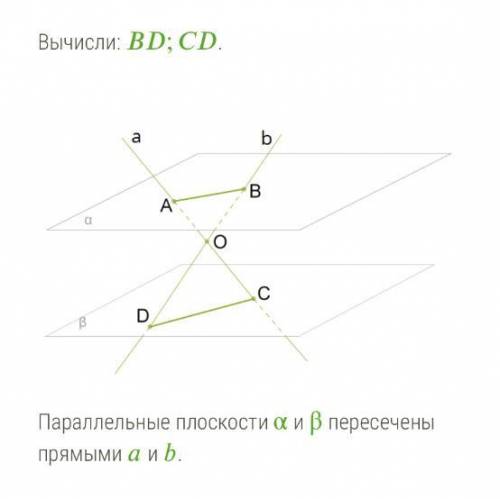
Вычисли: ;.

= см; = см.

Добрый день! Давайте рассмотрим данный вопрос.

У нас есть точка P, которая расположена между параллельными плоскостями α и β. Также имеются прямые и их отрезки, которые пересекают данные плоскости.

Для решения этой задачи, мы можем использовать знания о параллельных прямых и подобии треугольников.

Дано:
длина отрезка AD равна 15 см,
длина отрезка BC равна 27 см,
отрезок CF равен 3⋅.

На картинке представлен треугольник AFC, где отрезок AD принимает роль высоты этого треугольника. Так как прямые и параллельны, то мы видим, что треугольники AFC и BED подобны.

Находим высоту BE треугольника BED:
Используем свойство подобных треугольников: соответствующие высоты подобных треугольников образуют пропорцию.
BE/AD = BC/AF
BE/15 = 27/3⋅
BE/15 = 9
BE = 9 * 15
BE = 135 см

Теперь найдем отрезок DE:
DE = AD - BE
DE = 15 - 135
DE = -120 см

Очевидно, что отрезок не может иметь отрицательную длину, поэтому нам следует пересмотреть наше решение и убедиться, что мы не совершили ошибку.

Мы видим, что отрезок AD является высотой, а BC - основанием треугольника AFC. Поскольку эти два треугольника подобны и отрезки BC и DE соответствующие стороны этих треугольников, мы можем применить подобные пропорции.
BC/AD = DE/AF
27/15 = DE/3⋅
1,8 = DE/3⋅
DE = 1,8 * 3⋅
DE = 5,4⋅ см

Таким образом, мы нашли, что отношение длин отрезка BC к отрезку DE равно 1,8 : 3⋅ или, если привести результат к десятичному виду, 1,8 : 5,4.

Ответ:
DE = 5,4⋅ см.