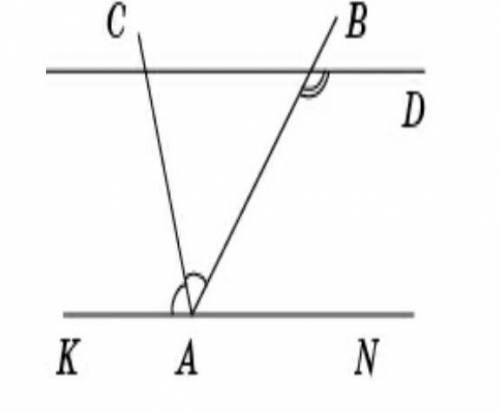
Через параллельные прямые CD и AK проведена секущая BA так, что угол ∠DBA = 130°. АС — биссектриса угла BAK. Найдите ∠CAB.
Решение.
Так как прямые CD// AK по условию, то ∠ ?= ∠KAB . Значит,
∠DBA = ∠ =_0 .
АС — биссектриса∠ ВАК по условию => ∠KAC = ∠ ?. Поэтому ∠CAB =∠ _ =_0 .
ответ: ∠CAB =__0 .
​

Гектор31    2   04.02.2021 00:45    13