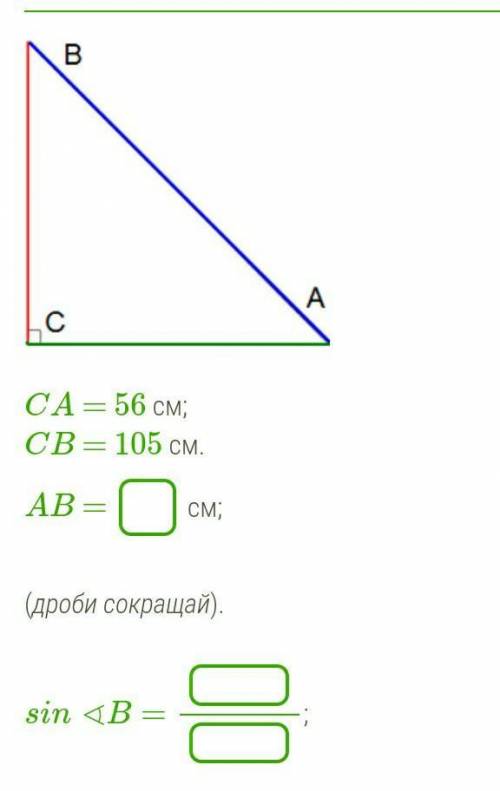
CA = 56 см;
CB = 105 см.

AB =  см;

 

(дроби сокращай).

sin∢B=;

  

cos∢B=.

​

Для решения этой задачи, нам необходимо использовать теорему синусов и теорему косинусов.

1. По теореме синусов, отношение длины стороны треугольника к синусу противолежащего ей угла одинаково для всех сторон треугольника. То есть, мы можем записать:
AB/sin∢A = BC/sin∢B = AC/sin∢C

2. Дано значение sin∢B. Нам нужно найти значение AB.
Используем теорему синусов: AB/sin∢A = BC/sin∢B
Заменяя значения, получаем: AB / sin∢A = 105 / sin∢B

3. Дано значение CB (105 см). Нам нужно найти значение AB.
Мы можем использовать теорему косинусов для решения этого:
AB² = AC² + BC² - 2 * AC * BC * cos∢A
Подставляем известные значения:
AB² = (56)² + (105)² - 2 * 56 * 105 * cos∢A

4. Найдем значение cos∢B.
Снова используем теорему косинусов:
BC² = AB² + AC² - 2 * AB * AC * cos∢B
Подставляем известные значения:
(105)² = AB² + (56)² - 2 * AB * 56 * cos∢B

Теперь у нас есть два уравнения с двумя неизвестными (AB и cos∢B). Мы можем решить это систему уравнений, чтобы найти значения этих неизвестных.

1. Подставим значение cos∢B из второго уравнения в первое уравнение:
AB/sin∢A = 105 / sin∢B
AB/sin∢A = 105 / sqrt(1 - (AB² + (56)² - (105)²) / (2 * AB * 56))
Где sqrt обозначает квадратный корень.

2. Разделим оба выражения на AB:
1/sin∢A = 105 / (AB * sin∢B * sqrt(1 - (AB² + (56)² - (105)²) / (2 * AB * 56)))

3. Подставим значение sin∢A из первого уравнения в полученное уравнение:
1 / (105 / sin∢B) = 105 / (AB * sin∢B * sqrt(1 - (AB² + (56)² - (105)²) / (2 * AB * 56)))

4. Упростим уравнение:
1 = (105)² / AB * sqrt(1 - (AB² + (56)² - (105)²) / (2 * AB * 56))

5. Умножим оба выражения на sqrt(2 * AB * 56):
sqrt(2 * AB * 56) = (105)² / AB * sqrt(1 - (AB² + (56)² - (105)²) / (2 * AB * 56))

6. Возведем оба выражения в квадрат:
2 * AB * 56 = (105)⁴ / (AB)² * (1 - (AB² + (56)² - (105)²) / (2 * AB * 56))

7. Упростим уравнение:
2 * AB * 56 = (105)⁴ / (AB)² - AB² - (56)² + (105)²

8. Соберем все члены вместе:
2 * AB * 56 + AB² + (56)² - (105)² = (105)⁴ / (AB)²

9. Полученное уравнение является нелинейным уравнением, которое можно решить численными методами или методом подстановки (проб и ошибок) для нахождения значения AB.

Таким образом, чтобы решить задачу, нам нужно решить систему уравнений из теоремы синусов и теоремы косинусов, а затем решать нелинейное уравнение для нахождения значения AB. Ответ будет зависеть от конкретных числовых значений, заданных в вопросе.