BP=10 PC=14 AP=биссектриса BK=? KD=? Приложил фотку с подробным объяснением.
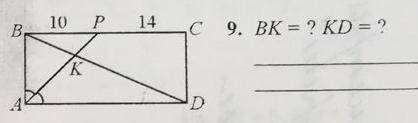
Другие вопросы по теме Геометрия
Популярные вопросы
- We often use just, yet, and already with the Present Perfect.Just...
1 - 1.почему Кыпчаки не смотря на многочисленность, не смогли противостоять...
2 - Индустриализация в Казахстане. Разгадав кроссворд вы получите ключевое...
1 - ЖАЗЫЛЫМ сөйлемдер құра.1-тапсырма. Берілген етістіктерді мақсатты...
3 - Як перехід до англіканство вплинув на королівську владу?...
3 - 1. Каким дан портрет Герасима? Опишите внешность героя близко к...
3 - Прочитай предложения, в пропущенные места вставь глаголы во времени...
1 - Сочинение рассужление по теме зачем нужно учиться...
3 - 1.Что относиться к экономическим последствиям завоеваниях монголов?...
1 - Что изображено на этом рисунке? что они делают...
1
- BC - это основание треугольника;
- AB и AC - боковые стороны треугольника.
Задача состоит в нахождении длин сторон BK и KD.
Мы знаем, что AP - это биссектриса угла BAC. Биссектриса делит угол на две равные части, поэтому между AB и AC делится на два угла одинаковой величины - BAD и DAC.
Используя данную информацию, мы можем применить теорему биссектрисы, которая говорит о том, что отношение длин сторон треугольника к длинам отрезков биссектрисы равно.
То есть, мы можем записать следующие соотношения:
AB/AP = BC/CP
AC/AP = BC/BP
Мы знаем, что BP = 10 и PC = 14, поэтому можем записать:
AB/AP = BC/14
AC/AP = BC/10
Можем выразить BC через AB и AP из первого соотношения:
BC = (AB*14) / AP
Подставим это выражение во второе соотношение:
AC/AP = ((AB*14)/AP) / 10
Теперь у нас есть уравнение с одной неизвестной переменной AB.
Упростим его:
AC/AP = (AB*14) / (AP*10)
Умножим обе части уравнения на 10*AP:
10*AC = AB*14
Поделим обе части на 14:
(10*AC) / 14 = AB
Таким образом, мы нашли длину стороны AB, она равна (10*AC) / 14.
Также мы знаем, что BK и KD - это отрезки, на которых основание треугольника BC делится биссектрисой AP.
Чтобы найти эти отрезки, можем использовать соотношение между длинами сторон треугольника и отрезками биссектрисы.
Имеем следующие соотношения:
BK = (AB*DC) / (AC + DC)
KD = (AC*DB) / (AB + DB)
Подставим значения AB и AC, которые мы нашли ранее:
BK = (((10*AC) / 14)*DC) / (AC + DC)
KD = (AC*DB) / ((((10*AC) / 14) + DB))
Теперь у нас есть формулы для нахождения длин отрезков BK и KD, используя известные значения BP, PC и AP.
После подстановки значений и выполнения всех вычислений можно получить конкретные числовые ответы.