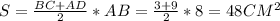боковые стороны ab и cd трапеции abcd равны соответственно 8 и 10, а большее основание ad равно 9. найдите площадь трапеции abcd, если известно, что биссектриса угла cda проходит через точку l, которая делит боковое ребро ab в отношении 9: 7, считая от большего основания.
Другие вопросы по теме Геометрия
Популярные вопросы
- Начало династии омейядов относится к какому году...
1 - 40 . напишите небольшой рассказ на тему наши - карты...
2 - Исравните в каждом слове произношение последнего парного согласного с...
1 - Напишите по образцу. (short)peter is the shortest boy in his class. (old)it...
2 - Пришло теплое лето. на лесной опушке распускаются колокольчики, незабудки,...
2 - Вкакой точке график функции у=2,5х-4 пересекает ось оу?...
3 - Отметь неравнества 4-2 1 5-2=3 1 5 4=4...
3 - Придумайте сами 2-3 занимательных по языку...
1 - Выразите в децеметрах и сантиметрах 42 см 23см 56см...
1 - Надо написать сочинение про описание: цвет, размер, форма, материал,...
3
48
Объяснение:
Продолжим боковые стороны трапеции (О - точка пересечения). Пусть OB = a, OC = b. В треугольнике AOD биссектриса делит сторону AO так, что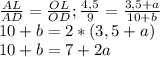
Поскольку в треугольнике AOD отрезок BC параллелен основанию AD (как основания трапеции), справедливо равенство:
Подставляем полученное выражение в найденное ранее:
То есть, ОВ = 4 и ОС = 5. Тогда имеем треугольник AOD со сторонами 9, 12 и 15 см => треугольник прямоугольный (подчиняется теореме Пифагора), и угол между сторонами AD и AB равен 90 градусов, и следовательно угол B также будет прямым.
Основание BC можно найти как катет в прямоугольном треугольнике OBC с катетом 4 и гипотенузой 5, оно будет равно 3 (по теореме Пифагора). В таком случае площадь трапеции равна произведению полусуммы оснований на высоту, т.е.