1. Геометрия
  2. Боковая сторона равнобедренного

Боковая сторона равнобедренного треугольника равна 4 см, а медиана проведенная к боковой стороне равна 5 см. найти радиус описанной около этого треугольника окружности?

OlesyaKotova1 OlesyaKotova1    3   27.08.2019 08:40    2

Ответы
Alle963 Alle963  05.10.2020 22:28
Примечание: x — основание, h – высота, проведённая к основанию, S – площадь треугольника, a – боковая сторона.
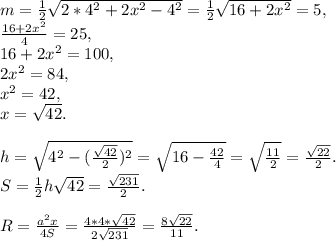
m = \frac{1}{2} \sqrt{2*4^2+2x^2-4^2} = \frac{1}{2} \sqrt{16+2x^2}=5, \\ \frac{16+2x^2}{4} = 25, \\ 16+2x^2 = 100, \\ 2x^2=84, \\ x^2 = 42, \\ x=\sqrt{42}. \\ \\ h = \sqrt{4^2 - ( \frac{ \sqrt{42} }{2} )^2}= \sqrt{16 - \frac{ 42 }{4} }= \sqrt{ \frac{11}{2} }= \frac{ \sqrt{22} }{2}. \\ S = \frac{1}{2}h \sqrt{42} = \frac{ \sqrt{231} }{2}. \\ \\ R = \frac{a^2x}{4S}= \frac{4*4* \sqrt{42}}{ 2\sqrt{231}} = \frac{8\sqrt{22}}{11}.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
mot1475 mot1475  04.02.2022 14:58
8 класс, признаки подобия треугольников , задача прикреплена ниже...
Abzik5203 Abzik5203  04.02.2022 15:03
В правильной четырехугольной пирамиде со стороной основания 12 найдите расстояние от высоты пирамиды до стороны основания...
bokshitskayan bokshitskayan  04.02.2022 15:07
ГЕОМЕТРИЯ РЕШИТЕ МИНИМУМ 4 ЗАДАЧИ...
bua20 bua20  04.02.2022 15:08
6. Точка М – основа висоти рівнобедреного трикутника АВС. За якої з наведених умов АВМ  СВМ ? а) АС – основа трикутника; б) ВС – основа трикутника; в) АВ – основа трикутника; г)...
mdebnu mdebnu  04.02.2022 15:12
На рисунке а||в, с- секущая. Найдите углы 1, 2, 3, 4, если 1 - 2 = 100...
mravals mravals  10.06.2019 05:10
Втреугольнике abc ab=2 см, bc=4 см, ac=5 см.1) найдите стороны подобного ему треугольника: а) def, зная, что большая его сторона равна 10 см;...
An0441 An0441  22.06.2019 20:40
Втреугольном треугольнике один катет больше другого в 3 раза,а гипотенуза равна 10 см.найдите меньший катет...
2806171 2806171  13.04.2019 20:28
На плоскости отметили все точки, равноудалённые от двух пересекающихся прямых. какое множество точек может оказаться отмеченным?...
arsenkam arsenkam  13.04.2019 21:59
Вравнобедренной трапеции abcd(ab=cd), описанной около окружности, высота bk равна 4 корня из 10 и делит большее основание в отношении 3: 7. найдите периметр трапеции....
jokjok1337 jokjok1337  13.04.2019 21:54
Там изображены 4 ребра, надо нарисовать шестиугольную пирамиду...

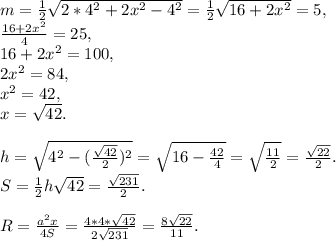
Популярные вопросы