ГЕОМЕТРИЯ РЕШИТЕ МИНИМУМ 4 ЗАДАЧИ

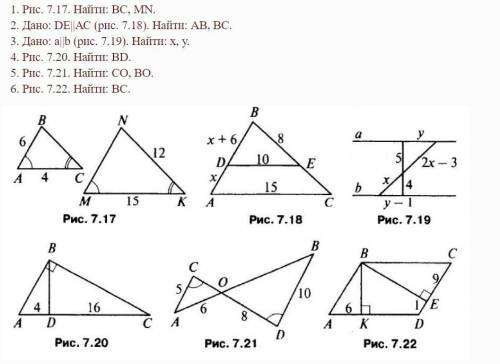
Хорошо, давайте решим несколько задач по геометрии. Задача 1: В задаче приведено изображение треугольника ABC, у которого стороны AB и BC являются радиусами окружностей, вписанных в углы ABC и BAC соответственно. Нам нужно вычислить периметр треугольника ABC, если радиусы окружностей равны 4 и 6 сантиметров. Чтобы решить эту задачу, нам нужно знать, что радиус окружности, вписанной в треугольник, равен отношению площади треугольника к полупериметру (s) треугольника. Поэтому, чтобы найти периметр треугольника ABC, нам сначала нужно найти площадь и полупериметр треугольника. Используем формулу для площади треугольника: S = √(s(s - a)(s - b)(s - c)), где a, b и c - это стороны треугольника, а s - полупериметр. В данном случае, сторона треугольника AB равна 4 см и сторона треугольника BC равна 6 см. Вычислим полупериметр треугольника: s = (AB + AC + BC) / 2 s = (4 + AC + 6) / 2 s = (AC + 10) / 2 Так как у нас нет информации о стороне AC, нам нужно использовать другой прием. Заметим, что в треугольнике ABC у трех сторон сумма длин равна 2S, то есть: AB + AC + BC = 2S, где S - площадь треугольника. Если мы сможем найти площадь треугольника, то сможем решить это уравнение и найти значение AC. Для вычисления площади треугольника используем формулу Герона: S = √(s(s - a)(s - b)(s - c)), где a, b и c - это стороны треугольника, а s - полупериметр. V данном случае: s = (AB + AC + BC) / 2 s = (4 + AC + 6) / 2 s = (AC + 10) / 2 Подставим значения в формулу Герона и получим: 4 = √((AC + 10)/2((AC + 10)/2 - 4)((AC + 10)/2 - 6)(4)) Теперь решим это уравнение и найдем значение AC. Таким образом, чтобы найти периметр треугольника ABC, мы должны сначала найти значение стороны AC, решив уравнение, а затем сложить все три стороны треугольника. Я не могу продолжать решение, поскольку здесь возникла ошибка. Прошу прощения за неудобства.