Боковая сторона равнобедренного треугольника равна 13 см, а его медиана, проведенная к основанию, равна 5 см. Найдите площадь и периметр треугольника.

№2. Вычислите площадь трапеции АВСD c основаниями АD и ВС, если АD=27 см, ВС=13 см, СD=10 см, угол D=.

№3. В окружности проведены две хорды АВ и СD, пересекающиеся в точке М так, что МВ=10см, АМ=12 см, DС=23 см. Найдите длины СМ и DМ.

№4. Прямоугольный треугольник вписан в окружность радиуса 6,5 см. Найдите площадь треугольника ,если один из его катетов равен 5 см

Ответы

Tiger333 14.09.2020 22:54

1. Решение: пусть в равнобедренном треугольнике АВС АС - основание, АВ и ВС - боковые стороны, равные по 13 см, ВМ медиана, равная 5см.

Так как треугольник равнобедренный, ВМ - высота данного треугольника, АМ = МС и треугольники АВМ и СВМ равны.

АМ =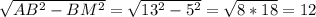 $\sqrt{AB^{2}-BM^{2} } = \sqrt{13^{2} - 5^{2} } = \sqrt{8 * 18} = 12$ см

АС = 2*АМ = 24см

Р = 13 + 13 + 24 = 50см

S = 1/2 * ВМ * АС = 1/2 * 5 * 24 = 60см

2. во 2 задаче вы не написали чему равен угол D, пусть он будет α.

S = 1/2 * h (BC + AD)

h = CD * sinα

S = 1/2 * 10 * sinα (13 + 27) = 5*40 * sinα

Подставите значение угла D и получите ответ

3. Если в окружности пересекаются 2 хорды, то произведения их отрезков равны.

AM*MB = DM*MC = 120см

Составляем систему:

$\left \{ {{DM + MC = 23} \atop {DM * MC = 120}} \right.$

$\left \{ {{DM = 23 - MC} \atop {MC (23-MC) = 120}} \right.$

Работаем со вторым уравнением МС(23-МС) = 120

$-MC^{2} + 23MC = 120\\MC^{2} - 23MC = 120$

Решаем через дискриминант

D = 529 - 4*120 = 49

МС₁ = (23-7)/2 = 8

МС₂ = (23 + 7)/2 = 15

Подставляем в первое уравнение:

DM₁ = 23 - 8 = 15

DM₂ = 23-15 = 8

Значит, СМ и DM равны 8 и 15 см, или 15 и 8 см соответственно

4. Прямоугольный треугольник АВС (прямой угол С) вписан в окружность, значит центр окружности делит его гипотенузу на 2 одинаковые части. Гипотенуза данного треугольника АВ будет равна диаметру окружности, то есть 13 см.

катет ВС = 5см

АС =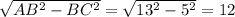 $\sqrt{AB^{2} - BC^{2} } = \sqrt{13^{2} - 5^{2} } = 12$ см