Без синусов, косинусов (если можете) - не проходили
Другие вопросы по теме Геометрия
Популярные вопросы
- Определите массу (1) воды, которую нужно добавить к растворумассой 50 гс массовой...
2 - ответы на во по литературе Гоголь поэма мёртвые души 1) как видит Гоголь Русь...
1 - ЗАПИШИТЕ МОЛЕКУЛЯРНУЮ И ИОННУЮ ФОРМУЛЫ Оксид серы(6) + угольная кислота...
2 - Гуморальний імунітет забезпечується...
1 - Найдите местоимения, сделайте их морфологический разбор.Составьте план и подготовьте...
1 - I. Add a question-tag to these sentences: 1. You are good at judo , ? 2. Jim has...
3 - Які висновки я зробив із твору «Чорнильне серце»?...
1 - C. Complete with the Past Simple Passive of the verbs in bracketsPeople thought...
3 - Как называется животных образовывать качественно новые свойства или качества в...
2 - B треуголькике PKT точка А принадлежит PK, точка B принадлежит KT, причём AB||PT....
3
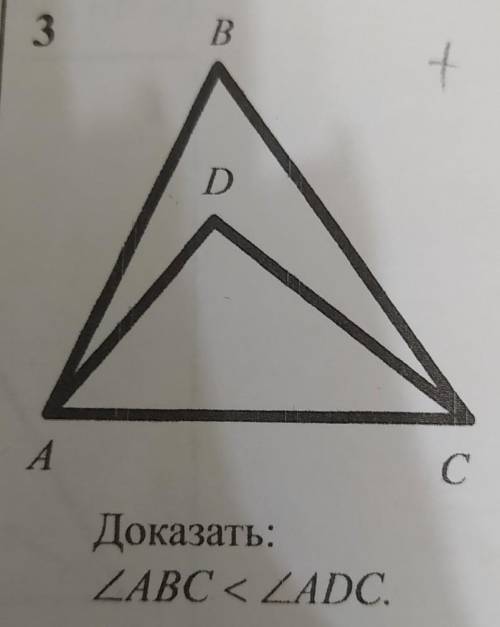
Итак, у нас дан следующий рисунок:
B
/|
/ |
/ |
8 / | 10
/ |
/ |
/ |
/_______|
A 6 C
Данный рисунок изображает прямоугольный треугольник ABC, так как угол ABC равен 90 градусов (угол прямой).
Первым шагом мы можем найти длину гипотенузы треугольника ABC (стороны AC) с использованием теоремы Пифагора, которая гласит: квадрат длины гипотенузы равен сумме квадратов длин катетов. В данной задаче катеты равны 6 и 8, поэтому:
AC^2 = 6^2 + 8^2 = 36 + 64 = 100
AC = √100 = 10
Теперь у нас есть длина стороны AC - 10 единиц.
Далее мы можем использовать соотношение между сторонами треугольника. Для прямоугольного треугольника это соотношение называется теоремой Талеса и утверждает, что отношение длин сторон прямоугольного треугольника всегда одинаково.
Так как стороны AB и BC относятся к основанию треугольника, они являются катетами и равны 6 и 8 соответственно.
Для того чтобы найти длину высоты BH, которая является высотой, опущенной из вершины B на гипотенузу AC, мы можем использовать соотношение между сторонами треугольников подобных друг другу.
С помощью теоремы Талеса мы можем записать:
BH/HC = AB/BC
Теперь мы можем подставить известные значения:
BH/HC = 6/8 = 3/4
Теперь мы можем найти высоту BH, умножив ее отношение к HC на длину HC = 10:
BH = (3/4) * 10 = 30/4 = 7.5
Таким образом, длина высоты BH равна 7.5 единицы.
Надеюсь, мой ответ был понятен и всеобъемлющим! Если у тебя возникнут еще вопросы, не стесняйся задать их!