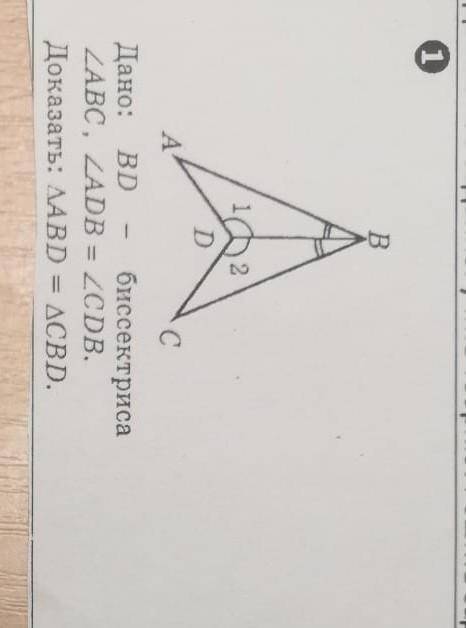
BD- биссектриса угла ABC, ADB=CDB, докажите что ABD=CBD

Для доказательства равенства углов ABD и CBD, мы должны использовать данные задачи и применить определенные свойства углов и треугольников.

Дано, что BD является биссектрисой угла ABC, а также что ADB равно CDB. Чтобы доказать, что углы ABD и CBD равны, мы можем воспользоваться свойствами углов, свойствами биссектрисы и свойствами треугольников.

1) Угол ABC разделен на два угла ABD и CBD биссектрисой BD.
- Свойство биссектрисы гласит, что она делит угол на два равных своими мерами угла.
- Мы знаем, что ABD и CBD очень похожи друг на друга, потому что они являются двумя частями одного и того же угла.

2) У нас есть также дано, что угол ADB равен углу CDB.
- Углы между параллельными прямыми, пересекающими третью прямую, являются соответствующими углами и равны друг другу.
- В данной задаче, прямая AB параллельна прямой CD, и биссектриса BD пересекает обе эти прямые. Таким образом, углы ADB и CDB являются соответствующими углами и равны друг другу.

Теперь, используя данные свойства и факты, мы можем сделать вывод, что углы ABD и CBD равны друг другу и сделать соответствующее пояснение для школьника:

"Итак, чтобы ответить на вопрос о равенстве углов ABD и CBD, мы можем воспользоваться следующими фактами:
1) BD является биссектрисой угла ABC, что означает, что этот угол разделен на два равных по величине угла - ABD и CBD.
2) Мы знаем, что угол ADB равен углу CDB, потому что эти углы являются соответствующими углами, образованными пересечением биссектрисы и параллельных прямых.
Поэтому, углы ABD и CBD равны, что и требовалось доказать".

Таким образом, мы подробно объяснили шаги решения и обосновали ответ, чтобы ответ был понятен школьнику.