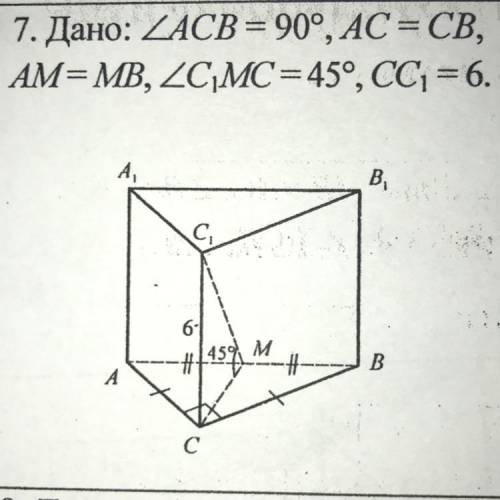
авса1в1с1-правильная треугольная призма, угол асв=90, ас=св, ам=мы, угол с1мс=45, сс1=6, найти объём призмы

Для вычисления объема треугольной призмы, нам необходимо знать площадь основания и высоту.

1. Определим площадь основания треугольной призмы.
Поскольку призма ABCD-A1B1C1D1 является равнобедренной, угол АСВ равен 90°, а отрезки АС и ВС равны между собой. Если мы узнаем длину отрезка АС, мы сможем найти площадь треугольника АСВ.

2. Определим значение отрезка АС.
По условию задачи, диагональ АМ равна диагонали А1М1 и угол С1МС равен 45°. Мы можем использовать эти данные, чтобы вычислить значение АС.

- Построим треугольник АМС, зная, что АС = ВС и АМ = М1М.
- Угол МАМ1 равен 45°, поскольку оба угла треугольника МАМ1 равны 45°.
- Также, угол АМС равен 45°, так как это основание изосцелесного треугольника.
- Таким образом, у нас есть прямоугольный треугольник АМС, в котором углы М, С и 45°.

Мы можем использовать теорему Пифагора для этого треугольника и получить следующее уравнение:

((МС)^2) = ((АМ)^2) + ((АС)^2)

- Подставим известные значения в уравнение.
((6)^2) = ((6)^2) + ((АС)^2)

- Решим уравнение.
36 = 36 + (АС)^2
0 = (АС)^2

Значит, АС равно 0.

3. Найдем площадь основания АВС.
Поскольку АС = 0, А и С совпадают, и треугольник АВС становится равносторонним.
Зная, что АВ = ВС = СА и S = (a^2 * sqrt(3)) / 4, где а - длина стороны треугольника, можем воспользоваться этой формулой для вычисления площади, где а будет равно 6 (поскольку АВ равно 6).

- Подставим известные значения в формулу.
S = (6^2 * sqrt(3))/4

- Вычислим площадь.
S = (36 * sqrt(3))/4
S = (9 * sqrt(3))/1

4. Найдем высоту призмы.
Так как призма равнобедренная, высота может быть найдена по теореме Пифагора.
Зная, что С1С = 6, СС1 = 6 и значит треугольник С1СС тоже является равносторонним, мы можем использовать его для вычисления высоты призмы, где х - высота призмы.

- Построим треугольник С1СС1, зная, что С1С = С1СС и CC1 = С1С.
- Так как треугольник равносторонний, все его стороны равны между собой.
- Таким образом, мы знаем длины всех сторон треугольника, они равны 6.

- Найдём высоту треугольника.
x = sqrt(6^2 - (6/2)^2) = sqrt(36 - 9) = sqrt(27) = 3*sqrt(3).

5. Вычислим объем треугольной призмы.
Теперь, когда у нас есть длина основания и высота призмы, мы можем вычислить объем призмы.
Формула для вычисления объема призмы: V = S * h.

- Подставим известные значения в формулу.
V = (9 * sqrt(3))/1 * 3*sqrt(3)

- Вычислим объем.
V = 27.

Таким образом, объем треугольной призмы составляет 27 кубических единиц.