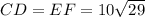АВС - прямоугольный треугольник с гипотенузой АВ. Из вершины С опущен перпендикуляр CD на гипотенузу. На отрезке CD как на диаметре построена окружность. Она пересекает стороны АС и ВС соответственно в точках Е и F. Найдите площадь треугольника АВС, если ЕС=50, FC=20.
Другие вопросы по теме Геометрия
Популярные вопросы
- Present simple, present continuous or past simple. 1. where (she/be)? i...
2 - (30 б.)почему рельеф южной америки преимущественно равнинный,а на западе...
3 - Количество вещества в 10 кг пищевой соды...
1 - Нужно создать вымышленую страницу в фэйсбуке печорина...
1 - определите относительную высоту объекта?...
3 - C6 h12 o6 h2 so4 найти массовую долю вещества...
2 - При взаимодействии фосфорной кислоты массой 34г с калием образовалось 34,5...
3 - 1. отметьте номера слов с ударением на втором слоге 1) закупорить 2) танцовщица...
2 - Какой поэтический образ повторяется в первом и во втором стихотворении?...
3 - Всети интернет найдите информацию о записи музыкальных произведений в формате...
3
ответ:4205
Объяснение:
По Теореме Пифагора: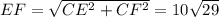
Значит,