1. Геометрия
  2. Abcd-квадрат sa перпендикулярно

Abcd-квадрат sa перпендикулярно (abc), о-середина ab найти угол между прямой so и asc, bc=8см sa=4 см

лооол19 лооол19    1   10.03.2019 02:20    0

Ответы
kisakz12 kisakz12  24.05.2020 13:24

Опустим из точки O на диагональ AC перпендикуляр OO'. При этом из теоремы о трех перпендикулярах (перпендикуляр SA к плоскости (ABC), наклонная SO', прямая OO' перпендикулярная AO') следует, что отрезок OO' перпендикулярен наклонной SO'. Тогда искомым углом будет угол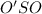 O'SO, обозначим его меру буквой x.

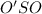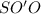 Из прямоугольного треугольника O'SO (угол SO'O равен 90 градусов по-доказанному) найдем sinx:

        sinx=\frac{OO'}{SO}-----(1)

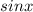   В свою очередь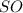 SO найдем из прямоугольного треугольника 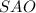SAO ( угол 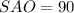SAO=90 градусов, что следует из определения прямой перпендикулярной плоскости) по теореме Пифагора:

    SO=\sqrt{SA^{2}+AO^{2}}=\sqrt{SA^{2}+\frac{BC^{2}}{4}} ------(2)

 

    где по условию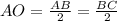 AO=\frac{AB}{2}=\frac{BC}{2} 

Из прямоугольного треугольника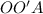 OO'A найдем

длину перпендикуляра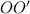 OO':

        OO'=AO*sin45=\frac{BC*sin45}{2}--------(3)

 

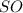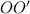И, наконец, подставим в (1) вместо SO и OO' выражения (2) и (3), получим:

           sinx=\frac{BC*sin45}{2\sqrt{SA^{2}+\frac{BC^{2}}{4}}}

Расчет:

     sinx=\frac{8*\frac{\sqrt{2}}{2}}{2*(\sqrt{16+\frac{64}{4}})}=\frac{1}{2}

 

  А значит угол O'SO=x=30 градусов 

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
katyasvk katyasvk  08.08.2019 19:10
Прямая параллельна стороне ав угла авс.пересекает ли она прямую вс...
markus10024 markus10024  08.08.2019 19:10
Точки d и е - середины сторон ав и вс треугольника авс, а точки м и n лежат на строне ас, причем ам=мn=nс, вектор ам= вектору a, вектор аd= вектору b. а) выразите векторы ае,...
sergiu21 sergiu21  08.08.2019 19:10
Втрапеции abcd боковые стороны равны 4 и 7см. p=24см. найдите среднюю линию трапеции....
guzhowa66 guzhowa66  08.08.2019 19:10
Решите : на стороне ад параллелограмма abcд взята точка м так что дм=дс , докажите что см - биссектриса угла с параллелограмма....
ТинкиВинкиДанки ТинкиВинкиДанки  12.04.2020 22:10
Найдите объем правильной четырехугольной пирамиды, если ее сечением, проходящей через высоту и диагональ основания, правильный треугольник со стороной 6√3 дм....
Саша1111111211111 Саша1111111211111  12.04.2020 22:23
Установить зависимость между площадью боковой поверхности цилиндра и площадью её развёртки. S Sбок...
volchica232005 volchica232005  12.04.2020 22:23
Задание 3. Дан параллелограмм АВСD. Построить фигуру F, на которою отображается данный параллелограмм при параллельном переносе на вектор cm .​...
KLerK11 KLerK11  12.04.2020 22:23
Дано: MN=KL=8,8см;∢MNO=60°....
sasgat sasgat  12.04.2020 22:23
В трапеции АВСД (АДII ВС) точка О – точка пересечения диагоналей АС и ВД, АО : ОС=5:2. Средняя линия трапеции равна 28 см. Найдите основания трапеции....
Опаснаятётя01 Опаснаятётя01  12.04.2020 22:24
по геометрии Сторона треугольника равна 12√29 , а две другие стороны образуют угол в 60° и относятся как 2:7. Найдите меньшую из этих двух сторон....

Популярные вопросы