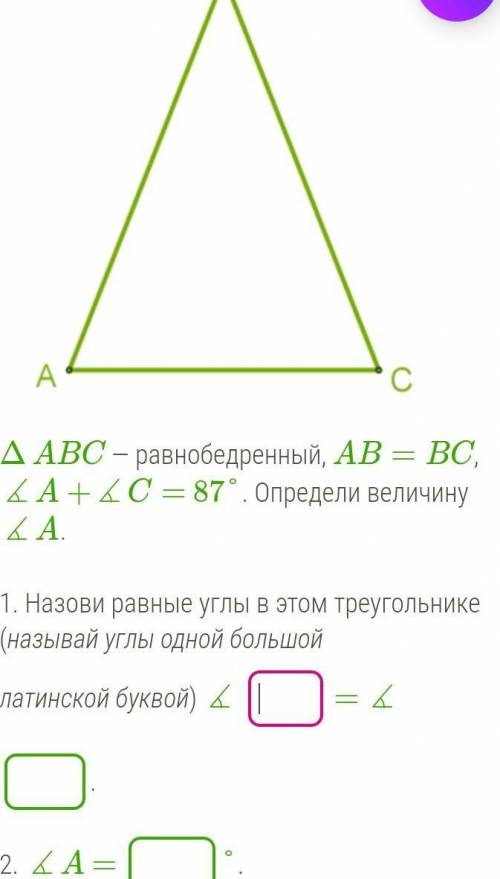
ΔABC — равнобедренный, AB=BC, ∡A+∡C= 87°. Определи величину∡A.
1. Назови равные углы в этом треугольнике (называй углы одной большой латинской буквой)
Другие вопросы по теме Геометрия
Популярные вопросы
- Побудувати графіки функцій, використовуючи елементарні перетворення:...
2 - Ребята тут такое дело два номера сделать 505 (1 , 2) и 602...
2 - Найдите для y=-x+16 функции точку пересечения с осью X. Нарисуйте...
1 - Побудуй прямокутник за діагоналлю та різницею двох сторін....
1 - На якій стадії фотосинтезу відбувається утворення глюкози...
1 - Тривалість імпульсу рубінового лазера 2мс. За цей час лазер випромінює...
2 - Номер 257. определите и запишите в таблицу недостающие данные...
1 - В тетраэдре DABC точка M отмечена в середине ребра DB. Дано,...
2 - Задание 8.Составить блок схему к задаче :Если первое число больше...
3 - США 19 веке конспект краткое...
2
В равнобедренном треугольнике углы при основании (в нашем случае ∠A и ∠C) всегда равны. Поэтому, если ∠A+∠C= 87°, то мы можем сказать, что ∠A= ∠C.
Теперь у нас есть два угла ∠A и ∠C, которые равны. Мы можем представить ∠A в виде х (где х - неизвестная величина) и заменить ∠C на ту же неизвестную величину. Таким образом, ∠A= ∠C= х.
Теперь нам нужно использовать свойство суммы углов треугольника. Сумма всех углов в треугольнике равна 180°. В нашем равнобедренном треугольнике у нас есть два равных угла (∠A и ∠C), поэтому мы можем записать уравнение:
∠A + ∠C+ ∠B = 180°
Так как ∠A= ∠C= х, то мы можем записать:
х + х + ∠B = 180°
Упрощая это уравнение, получаем:
2х + ∠B = 180°
Теперь нам нужно использовать информацию из задачи, что ∠A + ∠C = 87°. Заменяя ∠A и ∠C на х, получаем:
х + х = 87°
2х = 87°
Теперь мы можем решить это уровнение, разделив обе стороны на 2:
х = 87° / 2
х = 43.5°
Таким образом, величина ∠A равна 43.5°. Ответ: ∠A = 43.5°.