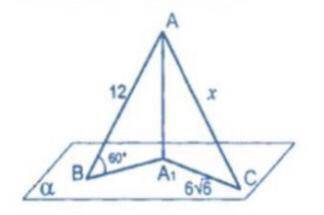
AA1-перпендикуляр к плоскости альфа, AB и AC- наклонные. Найдите x.

Для решения этой задачи нужно использовать свойства перпендикуляров и наклонных в плоскостях.

Первым шагом нам нужно понять, как связаны между собой перпендикуляр и наклонные. Из условия задачи мы знаем, что линия AA1 – перпендикуляр к плоскости альфа, а линии AB и AC – наклонные к этой плоскости.

При нахождении перпендикуляра к плоскости из точки A мы можем провести линии, перпендикулярные прямым AB и AC. Пусть эти перпендикуляры пересекают плоскость альфа в точках B' и C' соответственно.

Во-первых, заметим, что треугольники ABB' и ACC' являются прямоугольными треугольниками. В прямоугольных треугольниках угол 90 градусов образуется между основанием и гипотенузой. Так как BB' и CC' являются основаниями треугольников ABB' и ACC' соответственно, то угол между BB' и CC' также будет 90 градусов.

Во-вторых, треугольник ABC является прямоугольным треугольником, так как AA1 – перпендикуляр к плоскости альфа. Также из условия задачи нам дано, что угол BAC равен x градусов.

Теперь мы можем использовать свойства прямоугольных треугольников, чтобы найти значение x.

В треугольнике ABC угол BAC равен x градусов, а угол между основанием AC и гипотенузой AB равен 90 градусов. Таким образом, у нас есть два известных угла: x градусов и 90 градусов. Сумма углов в треугольнике равна 180 градусов, поэтому мы можем записать следующее уравнение:

x + 90 + угол между AB и BC = 180.

Так как угол между AB и BC равен 90 градусов, то мы можем записать новое уравнение:

x + 90 + 90 = 180.

Теперь мы можем решить это уравнение:

x + 180 = 180.

Вычтем 180 из обеих частей уравнения:

x = 0.

Таким образом, значение x равно 0.

Возвращаясь к исходной задаче, мы нашли, что значение x равно 0.