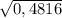Найти синус и косинус острого угла α , если а) sin α = 1/4 б) sin α √3/2 б) sin α = 0,72
Другие вопросы по теме Геометрия
Популярные вопросы
- Сборник язык страница 16 17 18 19 20 подскажите надо 4 класс...
2 - Выполните действие а+1/2а(а-1)-а-1/2а(а+1)...
2 - Из художественных произведений выпишите по два предложения с обращениями...
3 - Дайте определение следущим понятием подбирите 3-4 примера к ни: общеупотребительные...
2 - Zncl2+k2sio3=znsio3+2kcl разложите на ионы...
2 - Доказать, что среди шести любых чисел найдутся два, разность которых делятся...
3 - Скаким ускорением движется толо под действием силы 100h если под действием...
2 - Какие еще героические женские образы есть в эпосе других народов россии?...
3 - Через 20 с после начала движения электровоз развил скорость 4 м/с.найдите...
1 - Напишите 40 слов с безударной гласной в корне с проверочноми словоми...
2
Т.к. угол острый, то:
а) sin α = 1/4
ответ: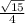
б) sin α √3/2
ответ: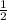
б) sin α = 0,72
ответ: