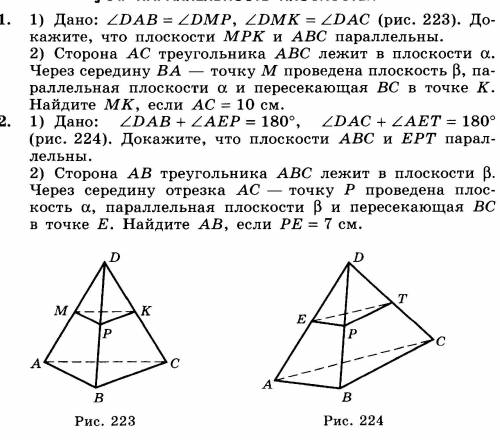
8.1)Докажите, что плоскости mpk и abc параллельны, если угол dab= углу dmp и угол dmk= углу dac Рис223

Привет! Я буду учителем и помогу тебе разобраться с этим математическим вопросом. Для начала, давай рассмотрим эту задачу. Нам нужно доказать, что плоскости mpk и abc параллельны, если угол dab равен углу dmp и угол dmk равен углу dac. Для начала, давай разберемся, что такое плоскости и углы. Плоскость - это пространственная фигура без толщины, она вытянута вдоль двух измерений (длины и ширины). Угол - это часть плоскости, ограниченная двумя лучами с общим началом, называемым вершиной угла. Итак, у тебя есть изображение, на котором показано, что угол dab равен углу dmp и угол dmk равен углу dac. Обрати внимание, что эти углы находятся на разных плоскостях: углы dab и dmp находятся на плоскости mpk, а углы dmk и dac находятся на плоскости abc. Теперь давай докажем, что плоскости mpk и abc параллельны. Для этого нам нужно показать, что перпендикулярные (пересекающиеся под прямым углом) прямые на одной плоскости не пересекают прямые на другой плоскости. У нас есть две пары углов, которые равны (углы dab и dmp, углы dmk и dac). Они находятся на разных плоскостях, поэтому мы не можем сказать, что перпендикулярные прямые на одной плоскости не пересекают прямые на другой плоскости. Таким образом, мы не можем доказать, что плоскости mpk и abc параллельны, и задача неразрешима. Надеюсь, я смог помочь тебе понять это математическое задание. Если у тебя есть еще вопросы, не стесняйся задавать их!