547. Найдите углы треугольника с вершинами в точках А(-1; 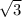 ), в(1; -), с (0,5; ).
), в(1; -), с (0,5; ).
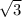
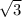
Другие вопросы по теме Геометрия
Популярные вопросы
- Тест по произведению М.А. Шолохова «Судьба человека». 1. Определите жанр...
3 - Стоимость экскурсии по Золотому Кольцу России составляет 6068 руб. Детям...
3 - Сколько минут в 15 градусах...
2 - 1. На другий склад падає наголос у всіх словах, ОКРІМА дичавітиБ проміжокВ...
2 - Напишите уравнения реакций, протекающих на катоде и аноде, а также общее...
1 - «Менің туған жерім» шығарма...
2 - МНОГО Внимательно прочитайте текст. ответьте на во связанные с текстом.Остров...
3 - Контрольная работа 8 класс,решите вариант....
1 - Построить в трёх тональностях (соль-диез минор, Ре-бемоль мажор, си-бемоль...
2 - - I m going toI m going toI d like to seeby ......
2
Для каждой вершины надо определить векторы сторон и их модули.
Угол А: векторы АВ и АС.
АВ = (1-(-1); -√3-√3)) = (2; -2√3), модуль равен √(4 + 12) = 4.
АС = (0,5-(-1); √3-√3) = (1,5; 0), модуль равен 1,5.
cos A = (2*1.5+( -2√3)*0)/(4*1.5) = 3/6 = 1/2.
Угол А = arccos(1/2) = 60 градусов.
Аналогично определяются другие углы.
Координаты векторов сторон
АВ BC (a) AС (b)
x y x y x y
2 -3,4641 -0,5 3,4641 1,5 0
Длины сторон АВ (с) = √(4+ 12) = √16 = 4
BC (а) = √(0,25+ 12) = √12,25 = 3,5
AC (b) = √(2,2+ 0) = √2,25 = 1,5.
Углы по векторам
cos A = (3+ 0)/ 6 = 0,5.
А = 1,0472 60 градусов
cos B = (1 +12)/ 14 = 0,9286.
В = 0,3803 21,7868 градуса
cos C = (-0,75 + 0)/ 5,25 = -0,14286
С = 1,71414 98,2132 градуса.
Можно проверить по теореме косинусов:
cos B = (a^2+c^2-b^2)/(2ac) = 26/ 28 = 0,928571429
B = arccos 0,9286 = 0,38025 радиан 21,7868 градуса/
cos C = (a^2+b^2-c^2)/(2ab)= -1,5/ 10,5 = -0,142857143
C = arccos -0,14286 = 1,714144 радиан 98,2132 градуса