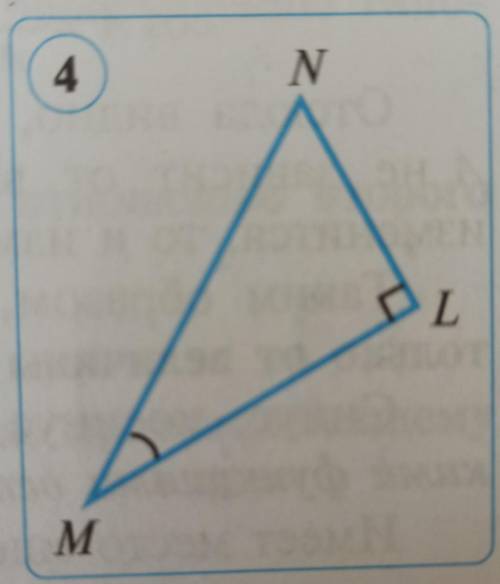
5. В прямоугольном треугольнике MNL sin N =24/25
Какие стороны треугольника можно найти из
этого равенства (рис. 4)?
​

Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.

Найти из этого равенства стороны невозможно, потому как в условии нет ни одного линейного размера. Например, стороны могут быть равны:

ML = 24, MN = 25

Или увеличенные в любое количество раз:

ML = 24 · 2 = 48;   MN = 25 · 2 = 50

ML = 24 · 3 = 72;   MN = 25 · 3 = 75

ML = 24 · 0,2 = 4,8;   MN = 25 · 0,2 = 5

ответ: зная только синус острого угла прямоугольного треугольника, невозможно найти ни одну сторону этого треугольника, можно только указать их отношение.

LM = 24 см

NM = 25 см

За т. Пифагора

NL = 7 см

sin N = ML ÷ MN (отношение противолежащего катета к гипотенузе) ⇒ ML ÷ MN = 24 ÷ 25, то есть длины ML и MN пропорциональны числам 24 и 25, то есть ML = 24x, MN = 25x

По теореме Пифагора находим:

NL² = MN² - ML²; NL² = (25x)² - (24x)² = (25x - 24x)(25x + 24x) = 49x² = (7x)² ⇒ NL = 7x

Исходя из условия задачи можно сделать вывод, что стороны

MN; NL; ML соответственно пропорциональны числам 25; 7; 24