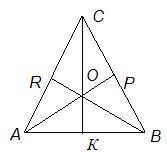
3. Докажите, что ∠САО = ∠СВО, если ОА = ОВ, а AK = BK.

Думала, думала и надумала)

1. Рассмотрим ΔAOC и ΔBOC: ∠AOC=∠BOC (по условию), AO=OB (по условию), CO - общая сторона. ΔAOC=ΔBOC (по двум сторонам и углу между ними), следовательно, CB=CA.

2. Рассмотрим ΔCQA и ΔCQB: CQ - общая сторона, CB=CA (из равенства выше), ∠BCQ=∠ACQ (CQ - биссектриса ∠C). ΔCQA=ΔCQB (по двум сторонам и углу между ними), следовательно, AQ=BQ ,∠ABC=∠BAC / что и требовалось доказать.

Объяснение: