На рисунке АВ||KD, поэтому треугольник DKC подобен треугольнику...
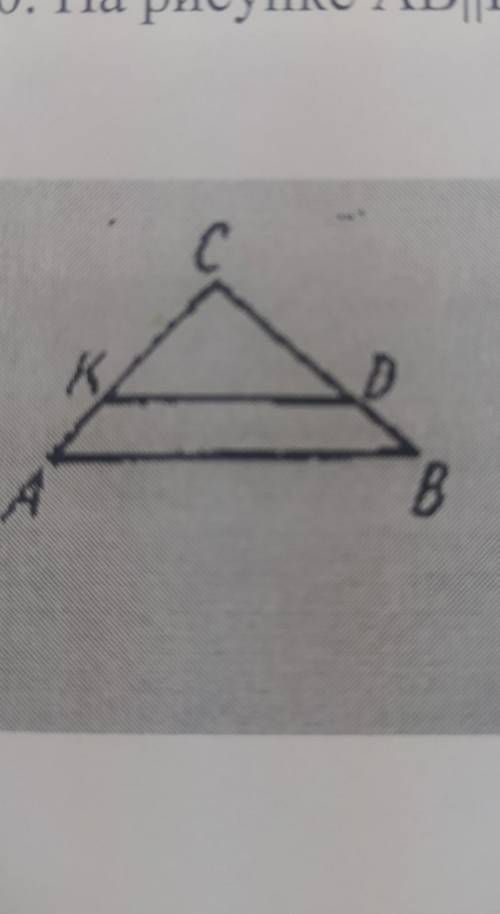
Другие вопросы по теме Геометрия
Популярные вопросы
- Две стороны треугольника равны 5/8 см с периметр 21/16см найди длину третей...
3 - евразия кеңістігіндегі көшпелілер эссе...
1 - Какой приём использует писатель при разделении общества на классы в рассказе...
1 - Для этана характерно(а) 1.одинарная связь между атомами углерода 2.наличие...
3 - Какова плотность подсолнечного масла если 1*0.001 м3 имеет 0,92 кг...
3 - Первые государства появились в средние века? да или нет?...
3 - Вмагазине нармина купила шёлковую ленту.для украшения шаров она отрезала 20...
1 - Составте предложение со словами расположение полагатся предложить изложение...
1 - Який діаметр ніхромового дроту довжиною 20 м якщо його опір 5 ом...
1 - Три целых четыре пятых тонн арбузов. в первый день продали 80%, во второй...
2
...ACB
Объяснение:
Когда говорят, что прямые АВ и КD параллельны, это означает, что они никогда не пересекутся и будут всегда находиться на одинаковом расстоянии друг от друга.
Теперь давайте рассмотрим треугольник DKC. Так как АВ и КD параллельны, то углы D и C образуют так называемую "Z" фигуру.
Аналогичная "Z" фигура образуется между углами A и K, так как прямые АВ и КD параллельны.
Для того чтобы убедиться, что треугольник DKC подобен треугольнику АBK, мы должны проверить, что соответствующие углы этих треугольников равны между собой.
В треугольнике DKC, угол KDC соответствует углу BAD треугольника АBK, так как они обе являются внутренними углами "Z" фигур.
Аналогично, угол DCK треугольника DKC соответствует углу ABK треугольника АВК, так как они обе являются внутренними углами "Z" фигур.
Итак, мы смогли установить, что углы KDC и BAD, а также углы DCK и ABK равны между собой.
Таким образом, мы пришли к выводу, что треугольник DKC подобен треугольнику АВК.
Чтобы подтвердить это, можно также проверить, что соотношение сторон треугольников DKC и АВК также подходит для подобия.