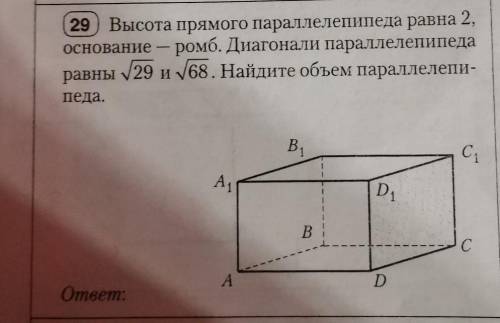
29 Высота прямого параллелепипеда равна 2, основание - ромб. Диагонали параллелепипеда
равны 29 и 68. Найдите объем параллелепи-
педа.​

Для решения данной задачи мы должны использовать знания о свойствах параллелепипеда и ромба. Итак, давайте разберемся.

Дано:
- Высота прямого параллелепипеда равна 2.
- Основание параллелепипеда - ромб.
- Диагонали параллелепипеда равны 29 и 68.

Нам нужно найти объем параллелепипеда.

Для начала, давайте разберемся с основанием параллелепипеда, которое является ромбом. Изображение ромба, которое дано в задаче, позволяет нам сделать вывод о том, что его диагонали перпендикулярны и пересекаются в точке O. Для решения задачи нам понадобится длина одной из диагоналей основания параллелепипеда - пусть это будет диагональ AD.

В параллелепипеде диагонали основания AD и DC пересекаются в точке O, которая является серединой диагонали AC. Поскольку AC - диагональ ромба и длина AC изображена на рисунке как 29, то длина диагонали AD (или DC) будет равна 29/2 = 14,5.

Теперь мы можем посчитать площадь основания параллелепипеда. Площадь ромба (S) можно вычислить, зная длины его диагоналей (d1 и d2), исходя из формулы:
S = (d1 * d2) / 2.

Подставим значения:
S = (29 * 68) / 2 = 986 квадратных единиц.

Теперь мы можем перейти к вычислению объема параллелепипеда. Объем параллелепипеда (V) равен произведению площади основания (S) на высоту (h):

V = S * h = 986 * 2 = 1972 кубических единиц.

Ответ: Объем параллелепипеда равен 1972 кубическим единицам.