2. в четырехугольнике abcd к диагонали ас проведены перпен-
дикуляры bf и dk, причем bf = dk, угол baf = угол dck. докажите,
что abcd – параллелограмм.
tsartsar
3
03.09.2019 14:15
30
Другие вопросы по теме Геометрия
danek20063
30.10.2020 10:00
kogoch
30.10.2020 10:00
Дильназ231
30.10.2020 10:00
drad2005
30.10.2020 10:00
mirator91
16.01.2021 16:38
savannah1
16.01.2021 16:37
кек946
16.01.2021 16:34
Lianda2007
16.01.2021 16:31
Популярные вопросы
- Что означает фамилия Хрюкін когда они Хамелеон...
3 - Изображение десятичных дробей на координатном лу дробей. Урок 1Запиши координату...
3 - Скільки цілих невід’ємних чисел, менших за мільйон, можна записати за до цифр:...
2 - Какие проблемы современного воспитания сейчас существуют?Приведите не менее...
1 - Какова вероятность того, что из 3000 студентов колледжа 12 родились 10 августа?...
2 - Hola, soy Lucas y tengo doce años. En casa somos cinco personas. Mi madre...
2 - Essay about the transports in the future. эссе на тему «транспорты будущего...
3 - Обчисліть всі сторони трикутника MCF якщо MC більша від CF на 6 см а периметр...
3 - геометрия 7 класс решить вопрос жизни и смерти очень вас умные светлые умы...
2 - честно сделайте я серьезно...
2
Прямоугольные треугольник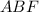и
и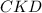 
равны по катету и прилежащему острому углу (
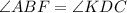). Из равенства треугольников следует, что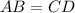 
Так как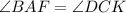
- накрест лежащие углы равны, то по первому признаку параллельности прямых 
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.Следовательно,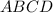
- параллелограмм.