1.В треугольнике ABC угол С прямой, угол А равен 42°, AB=8 см. Найдите АС и СВ.

2.У прямоугольного треугольника один катет равен 8см, а гипотенуза равна 15 см. Найдите другой катет и острые углы треугольника.

3.В треугольнике МКС угол С прямой, угол М равен 70°, MC =8 см. Найдите МК и СК.

Ответы

SoftMGDN 20.04.2021 16:49

Синус угла A — равен: AB/CB.

Так как угол нам уже известен(42°), то его синус найдём по таблице: 0,6691.

Тоесть — катет CB равен: 0.6691*8 = 5.353.

Катет AC — найдём по теореме Пифагора: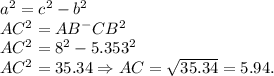 $a^2 = c^2-b^2\\AC^2 = AB^-CB^2\\AC^2 = 8^2-5.353^2\\AC^2 = 35.34 \Rightarrow AC = \sqrt{35.34} = 5.94.$

Вывод: AC = 5.94; CB = 5.353.

Второй катет равен(по теореме Пифагора):

$b^2 = c^2-a^2\\b^2 = 15^2-8^2\\b^2 = 161 \Rightarrow b = \sqrt{161} = 12.7.$

Второй катет равен: 12.7.

Найдём углы по их тангенсам.

Тангенс угла А равен: противоположный катет делить на прилежащий катет.

У нас есть треугольник ABC(прямой угол — C), по нашим расчётам — AB = 15; AC = 8; BC = 12.7.

$tg(\alpha) = BC/AC = 12.7/8\\tg(alpha) = 1.5875 \Rightarrow$

Вывод: <B = 33°; <A = 57°.

<M = 70° => <K = 90-70 = 20°.

Формула вычисления катета, зная гипотенузу, и угол прилежащего катета таков:

$a = b*tg(\alpha)\\KC = MC*tg(70^o)\\tg(70^o) = 2.7475\\KC = 8*2.7475\\KC = 21.98.$

Гипотенузу найдём по теореме Пифагора:

$c^2 = a^2+b^2\\c^2 = 8^2+21.98^2\\c^2 = 64+483.12\\c^2 = 547.12 \Rightarrow c = 23.4.$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

yuliana080704 03.09.2019 07:30

DeltaMintz 03.09.2019 07:30

IrinaArinaRina 03.09.2019 07:30

Ḱặрặṃềӆьҟӑ 03.09.2019 07:30

ыфыфыф553 06.07.2019 18:20

alinka57d 01.06.2019 23:40

Масянька189 01.06.2019 23:40

Юрашевич101 01.06.2019 23:30

Aruzhankaaaaa1 01.06.2019 23:30

slarina171 01.06.2019 23:30