1. в правильную треугольную пирамиду вписан конус. найти площадь боковой поверхности этого конуса, если известно, что боковые грани пирамиды наклонены к плоскости основания под углом в 60 град. и радиус круга, вписанного в основание пирамиды, равен 16. 2. определить tg(бета), где (бета) - внутренний угол правильного шестиугольника. решить и понять суть , заранее .
Другие вопросы по теме Геометрия
Популярные вопросы
- Подайте произведение (4 +х )(х − 4) в виде многочлена....
2 - 25 . доклад на тему : колокола моего города ( санкт-петербург )...
1 - Почему природные зоны евразии и северной америки имеют много общего...
1 - Из воронежа в москву вышел пассажирский поезд со скоростью 60 км/ч. одновременно...
2 - Маленький шарик массой 0,4 г подвешен на тонкой шелковой нити и имеет заряд 4...
2 - Спільно кореневої слова до слова сонце...
3 - От станции одновременно в противоположных направлениях отправились два поезда...
3 - Замените в числе * так, чтобы число 27*52*6 делилось на 9....
2 - 25 ! вставь пропущенные слова this,these,that, those. town is old but nice and...
2 - За конфеты заплатили в 3 раза больше, или на 28,6 д.е. больше, чем за печенье....
1
Решение в приложенном рисунке
Попробовал расширение JPG - не
1 Площадь боковой поверхности конуса равна пи*радиус основания(r)* апофему(l)(отрезок соединяющий точку окружности основания и вершину конуса). Радиус основания =16 по условию. Апофему находим через определение косинуса. Высота конуса, апофема и радиус основания образуют прямоугольный треугольник с углами 90, 60 (по условию) и 30 градусов (сумма углов треугольника=180 градусов)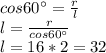
Площадь боковой поверхности=π*r*l=π*16*32=512*π
2 по определению-внутренние угль правильного шестиугольника=120 градусов