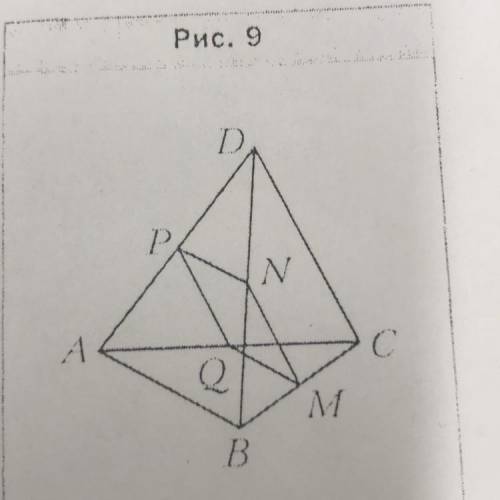
1. Точки M, N, Р и Q - середины отрезков BC, BD, AD и AC соответственно, AB = 14 см, CD = 18 см (рис.9). Определите вид
четырёхугольника MNPQ и вычислите его периметр.

32 см

Объяснение:

Дано:

Точки M, N, Р и Q - середины отрезков BC, BD, AD и AC;

AB = 14 см, CD = 18 см

Определить: вид MNPQ.

Найти: Р (MNPQ)

1. Рассмотрим ΔBDC.

BN = ND; BM = MC (условие)

⇒MN - средняя линия.

Средняя линия треугольника параллельна основанию и равна его половине.

⇒ MN || DC;

MN = DC:2 = 18 :2 = 9 (см)

2. Рассмотрим ΔADC.

AP = PD; AQ = QC (условие)

⇒ PQ - средняя линия.

⇒ PQ || DC;

PQ = DC : 2 = 18 :2 = 9 (см)

3. Рассмотрим MNPQ.

Если две прямые параллельны третьей, то они параллельны между собой.

⇒ PQ || NM

При этом PQ = NM

Если две противоположные стороны четырехугольника равны и параллельны, то этот четырехугольник - параллелограмм.

⇒ MNPQ - параллелограмм.

4. Рассмотрим ΔADB.

AP = PD; BN = ND (условие)

⇒ PN - средняя линия.

PN = AB : 2 = 14 : 2 = 7 (см)

5. Найдем периметр.

Противоположные стороны параллелограмма равны.

⇒ QM = PN = 7 см.

QP = MN = 9см

Периметр параллелограмма равен удвоенной сумме смежных сторон.

Р (MNPQ) = 2*(QP+QM) = 2(7 + 9) = 32 (см)