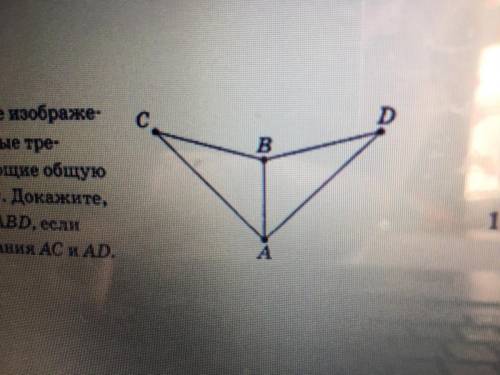
1. На рисунке изображе- ны равнобедренные тре-
угольники, имеющие общую
боковую сторону. Докажите,
что треугольник ABC - треугольнику ABD, если
равны их основания AC и
AD.

Чтобы доказать, что треугольники ABC и ABD равны между собой, нам нужно рассмотреть свойства равнобедренных треугольников и применить их к данной ситуации.

Свойство 1: Равнобедренный треугольник имеет две равные стороны, называемые равными боковыми сторонами.

На рисунке даны два равнобедренных треугольника ABC и ABD, имеющие общую боковую сторону AB. Это означает, что стороны AC и AD должны быть равными.

Мы должны доказать, что треугольники ABC и ABD равны между собой. Для этого нам нужно сравнить их остальные стороны и углы.

1. Сторона AB: Обе стороны ABC и ABD имеют общую боковую сторону AB, поэтому их длины равны.

2. Сторона AC: Нам уже известно, что сторона AC треугольника ABC равна стороне AD треугольника ABD. Это означает, что сторона AC и сторона AD равны между собой.

3. Сторона BC: Мы не знаем, что именно представляет собой сторона BC, но мы можем использовать свойство равнобедренного треугольника. Равнобедренный треугольник имеет два равных угла между двумя равными сторонами. Так как у треугольников ABC и ABD есть общая боковая сторона AB и равные основания AC и AD, то у них также есть равные углы между этими сторонами. Следовательно, угол BAC треугольника ABC будет равен углу BAD треугольника ABD.

На данный момент, у нас есть равные стороны AB и AC/AD, а также равные углы BAC и BAD. Это означает, что у нас есть два равнобедренных треугольника ABC и ABD.

Следовательно, мы можем сделать вывод:
Треугольники ABC и ABD равны между собой на основании равных их оснований AC и AD.

Это было доказательство того, что треугольники ABC и ABD равны друг другу.