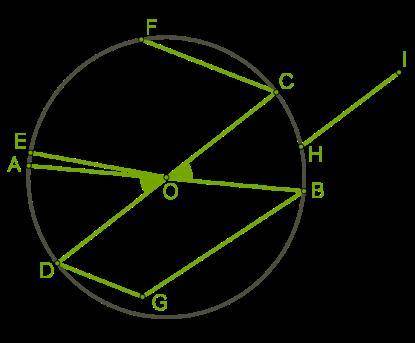
1. Дана окружность и несколько отрезков. Которые из них радиусы, хорды, диаметры? Радиусы
DO
CF
BG
HI
CO
BA
EO
CD
AO
DG
BO

Хорды
CO
HI
BA
BG
AO
DO
BO
CF
CD
DG
EO

Диаметры
DG
CF
DO
BO
CD
AO
BA
CO
EO
BG
HI

2. Если EO = 16 см, то BA =
см.

Давай начнем с объяснения основных понятий, связанных с окружностью.

1. Радиус (R) - это отрезок, который соединяет центр окружности с ее любой точкой на границе. На изображении данной задачи, радиусы обозначены буквами: DO, CF, BG, HI, CO, BA, EO, CD, AO, DG, BO.

2. Хорда (CH) - это отрезок, который соединяет две точки на границе окружности. Хорда не проходит через центр окружности. На изображении задачи, хорды обозначены буквами: CO, HI, BA, BG, AO, DO, BO, CF, CD, DG, EO.

3. Диаметр (D) - это самая длинная хорда окружности, проходящая через ее центр. Диаметры обозначены буквами: DG, CF, DO, BO, CD, AO, BA, CO, EO, BG, HI.

Теперь, возвращаясь к задаче:

1. Исходя из определений, можем ответить на вопросы о характере каждого отрезка:

- Радиусы:
DO - радиус, так как он соединяет центр окружности (точку O) с точкой на границе (такая конструкция есть только у радиуса).
CF, BG, HI, CO, BA, EO, CD, AO, DG, BO - не являются радиусами, так как не соединяют центр окружности с точками на границе, а просто отрезки, рассматриваемые на этой окружности.

- Хорды:
CO, HI, BA, BG, AO, DO, BO, CF, CD, DG, EO - являются хордами, так как соединяют две точки на границе окружности.

- Диаметры:
DG, CF, DO, BO, CD, AO, BA, CO, EO, BG, HI - являются диаметрами, так как проходят через центр окружности и являются самыми длинными хордами.

2. Для решения второго вопроса, нам дано, что EO = 16 см. Мы должны найти значение BA.

На основе определений радиуса и хорды, мы знаем, что радиус (EO) перпендикулярен хорде (BA), проходящей через точку пересечения радиуса и хорды. Также мы знаем, что радиус делит хорду пополам.

Следовательно, мы можем сделать вывод, что BA = 2 * EO = 2 * 16 см = 32 см.

Итак, мы получаем, что BA равно 32 см.

Надеюсь, это решение будет понятно школьнику. Если у него возникнут дальнейшие вопросы, он всегда может обратиться ко мне за помощью.