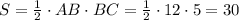1. дан треугл. mnk - равносторонний, со стороной 8 см ( какая сторона, не указана ), найти : r - радиус. 2. дан треугл. авс - прямоугольный, вписан в окружность, r = 6,5 см, один из катетов = 5 см, найти площадь треугольника! можете ещё и с рисуночком,скинуть, ..**
Другие вопросы по теме Геометрия
Популярные вопросы
- Составьте синквейн про признаки равенста треугольников. нужно!...
2 - Сформулировать правило на правописание слов с окончанием шь (например...
3 - 5в квадраті помножити на 8 в кубі, надо...
2 - Особенности взаимодействия музыки и...
3 - Опишите кокованю из серебряного копытца...
3 - Как называется совокупность особей одного вида с общим генофондом...
3 - Впаровой турбине для совершения работы используется 1/10 часть...
3 - Всуде слушается дело по поводу высказывания алиментов. мать имеет...
3 - Подскажите . где можно найти хороший доклад по обж? на тему:...
3 - А.н. островский гроза . с позиции вашего понимания характера...
2
Нарисовать не смогу, но опишу.
1.Соедени центр окружности с вершинами треугольника (как сама понимаешь - это радиусы окружности). Вспомни что что сумма получившихся трёх центральных углов - 360 градусов.) Ах, да! Тиарема Пифагора тебе
2. S=1/2 *5 * SQRT(13^2 - 5^2)
Решение. Т.к. ΔMNK – равносторонний, то радиус вписанной окружности ищется по формуле
Радиус описанной окружности
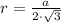
2. Дан треугл. АВС - прямоугольный, вписан в окружность, R = 6,5 см, Один из катетов = 5 см, Найти площадь треугольника!Можете ещё и с рисуночком, скинуть
Решение. Пусть ВС = 5 см. Т.к. ОС = R = 6,5 см, то АС = 2ОС = 13 см.
По т.Пифагора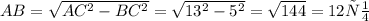
Тогда