Впустой калориметр влили ложку горячей жидкости, после чего температура калориметра увеличилась на δt1 = 5°с. затем в него влили вторую такую же ложку жидкости, и температура калориметра увеличилась на δt2 = 3°с. на сколько градусов δt увеличится температура калориметра после вливания в него такой же третьем ложки?

Ответы

daravill1 08.10.2020 14:27

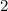ответ: °С

Объяснение:

Дано:

$зt_{1} = 5$ °С

$зt_{2} = 3$ °С

------------------

$зt_{3} -?$

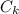Пусть $C_{k}$ - теплоемкость калориметра

- теплоемкость воды в ложке

$t_{H}$ - начальная температура калориметра

$t_{k}$ - конечная температура калориметра

- температура воды в ложке

Теперь запишем уравнение теплового баланса после того как мы влили первую ложку воды в пустой калориметр

$Q_{pol1} = Q_{otd1}$

$C_{k} (( t_{H} + зt_{1}) - t_{H} ) = C( t - (зt_{1} +t_{H} ))$

$C_{k}зt_{1} = C( t - зt_{1} -t_{H} )$ - уравнение (1)

Аналогично и для второго случая

$Q_{pol2} = Q_{otd2}$

$C_{k} (( t_{H} + зt_{1} + зt_{2}) - t_{H} ) = 2C( t - (зt_{1} + зt_{2}+t_{H} )$

$C_{k} ( зt_{1} + зt_{2} ) = 2C( t - зt_{1} - зt_{2}-t_{H} )$ - уравнение (2)

В уравнении (2) фигурирует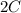 так как это уже "вторая ложка"

Получаем систему из уравнений (1) и (2)

$\left \{ {{C_{k}зt_{1} = C( t - зt_{1} -t_{H} )} \atop {C_{k} ( зt_{1} + зt_{2} ) = 2C( t - зt_{1} - зt_{2}-t_{H} )}} \right.$

Разделим уравнение уравнение (1) на (2)

$\dfrac{C_{k}зt_{1}}{C_{k} ( зt_{1} + зt_{2})}= \dfrac{C( t - зt_{1} -t_{H} )}{ 2C( t - зt_{1} - зt_{2}-t_{H} }$

Подставляя численные значения упростим

$\dfrac{5}{5 + 3}= \dfrac{t - 5 -t_{H} }{ 2( t - 5 - 3-t_{H}) }$

$10( t - 8-t_{H})= {8(t - 5 -t_{H})$

$10t - 80-10t_{H}= 8t - 40 -8t_{H}$

$2t -2t_{H} =40$

$t -t_{H} =20$ °С

Тогда подставляя это в уравнение в уравнение (1) получим

$C_{k}зt_{1} = C( 20 - зt_{1} )$

$5C_{k} = 15C$

$C_{k} = 3C$

После вливания в калориметр третьей ложки получим что

$C_{k} (t_{k} - t_{H})=3C(t-t_{k} )$

$3C (t_{k} - t_{H})=3C(t-t_{k} )$

$t_{k} - t_{H}=t-t_{k}$

$2t_{k} =t + t_{H}$

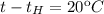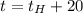
Если $t -t_{H} =20 кC$ то $t= t_{H} +20$

$2t_{k} =2 t_{H} + 20$

$t_{k} - t_{H}= 10$ °С

Допустим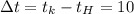 $зt = t_{k} - t_{H}= 10$ °С

Тогда

$зt=зt_{1}+зt_{2}+зt_{3}$

$зt_{3}=зt-(зt_{1}+зt_{2})$

$зt_{3}=10-(5+3) = 2$ °С

ПОКАЗАТЬ ОТВЕТЫ

Крошка21155 09.01.2024 01:17

Добрый день! Давайте решим эту задачу вместе.

Для начала, давайте рассмотрим, как меняется температура калориметра при вливании первой и второй ложки жидкости.

По условию, при вливании первой ложки жидкости температура калориметра увеличилась на δt1 = 5°С. Давайте обозначим начальную температуру калориметра до вливания первой ложки как T0. Тогда температура калориметра после вливания первой ложки будет равна T1 = T0 + δt1.

Теперь рассмотрим вторую ложку жидкости. По условию, при вливании второй ложки температура калориметра увеличилась на δt2 = 3°С. Давайте обозначим температуру калориметра после вливания первой ложки (T1) как начальную температуру перед вливанием второй ложки. Тогда температура калориметра после вливания второй ложки будет равна T2 = T1 + δt2.

Теперь у нас есть две известные позиции: начальная температура калориметра (T0) и температура после вливания второй ложки (T2). Нам нужно найти, на сколько градусов δt изменится температура калориметра после вливания в него третьей ложки.

Чтобы это сделать, давайте рассмотрим разность между T2 и T0. ΔT = T2 - T0. Зная это значение, мы сможем найти δt, на сколько увеличится температура калориметра после вливания третьей ложки.

ΔT = T2 - T0 = (T1 + δt2) - T0

Осталось подставить известные значения: T1 = T0 + δt1 и δt2 = 3°С

ΔT = (T0 + δt1 + δt2) - T0
ΔT = (T0 + 5°С + 3°С) - T0

Теперь объединим все элементы, содержащие T0:
ΔT = (T0 - T0) + (5°С + 3°С)
ΔT = 0 + 8°С
ΔT = 8°С

Таким образом, температура калориметра увеличится на 8°С после вливания третьей ложки жидкости.

Надеюсь, мой ответ понятен. Если у вас остались какие-либо вопросы, пожалуйста, задайте их.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Физика