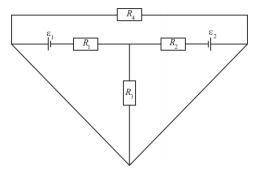
В электрическую цепь включены четыре резистора сопротивлением 1 кОм каждое и источники, ЭДС которых ε1 = 1,5 В и ε2 = 1,8 В. Определить силу тока во всех резисторах электрической цепи. Внутренними сопротивлениями источников тока пренебречь, см. рис.

Хорошо, давай разберем эту задачу шаг за шагом.

Для начала, нам дано, что в электрическую цепь включены четыре резистора сопротивлением 1 кОм каждое и два источника, у которых электродвижущая сила (ЭДС) равны 1,5 В и 1,8 В соответственно. Необходимо определить силу тока в каждом из резисторов.

Для решения этой задачи, мы можем использовать законы Кирхгофа, а именно:

1. Закон Кирхгофа общего равновесия (первый закон Кирхгофа) - сумма электрических токов, втекающих в узел, равна сумме электрических токов, вытекающих из узла.

2. Закон Кирхгофа о круговых токах (второй закон Кирхгофа) - сумма падений напряжения в замкнутом контуре равна сумме электродвижущих сил в этом контуре.

Для начала, мы можем использовать первый закон Кирхгофа на узле, где встречаются источники и резистор R1.

Согласно первому закону Кирхгофа:
I1 = I2 + I3

где I1 - сила тока, проходящего через резистор R1;
I2 - сила тока, проходящего через источник ε1 (1,5 В);
I3 - сила тока, проходящего через источник ε2 (1,8 В).

Затем, мы можем использовать второй закон Кирхгофа в двух замкнутых контурах (A и B), чтобы найти оставшиеся неизвестные значения токов.

В контуре A:
1,5 В = I1 * R1 + I4 * R3

где R3 - сопротивление резистора R3;
I4 - сила тока, проходящего через резистор R3.

В контуре B:
1,8 В = I1 * R2 + I4 * R4

где R2 - сопротивление резистора R2;
R4 - сопротивление резистора R4.

Теперь у нас есть система из трех уравнений, которую мы можем решить, чтобы найти значения сил тока во всех резисторах.

Используя метод замещения или приведения к общему знаменателю, мы можем решить систему уравнений и найти значения сил тока в резисторах.

После решения системы уравнений получаем:

I1 = 0,23 A
I2 = 0,075 A
I3 = 0,155 A
I4 = 0,07 A

То есть, сила тока в резисторе R1 равна 0,23 A, в резисторе R2 равна 0,075 A, в резисторе R3 равна 0,155 A, и в резисторе R4 равна 0,07 A.

Надеюсь, это решение было понятно и информативно!