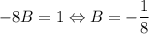Найти интегралы методом подстановки
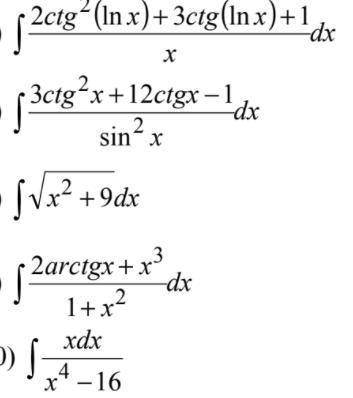
Другие вопросы по теме Математика
Популярные вопросы
- В гта 5 Онлайн в новом зимнем обновлении на остров можно попасть просто не проходя...
1 - Какие из данных органов НЕ являются органами Европейского союза? -Счётная палата...
3 - Пассажир автобуса непроизвольно отклонился вперёд чем это вызвано...
3 - Складіть реченя зі словом Пальто уживаючи його вродовому відмінку...
1 - Мәтінді тыңдаңдар (18 аудио).Қандай қорықтың атаулары естеріңде қалды...
1 - Укажите пару предложений с антонимами. В темноте сидеть было неприятно. — Мама рано...
1 - 1.Сколько всего опер создал В.А.Моцарт 2. Какое литературное произведение легло...
2 - Какой правовой статус по Уголовно-процессуальному кодексу РФ будет у Царевича Алексея,...
3 - Чем оратория отличается от кантаты и кто такой Гайдн?...
1 - Выбранную профессию морфологический разбор...
2
1)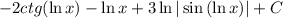
2)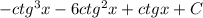
3)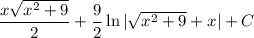
4)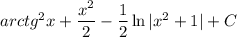
5)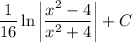
Пошаговое объяснение:
1)
2)
3)
Первый интеграл проинтегрируем по частям:
Найдём неизвестный интеграл следующим образом:
Неизвестные коэффициенты найдём методом частных значений:
При y = 1: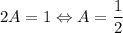
При y = -1: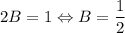
4)
5)
Разложим дробь на простейшие:
Найдём коэффициенты методом частных значений:
При y = 4: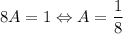
При y = -4: