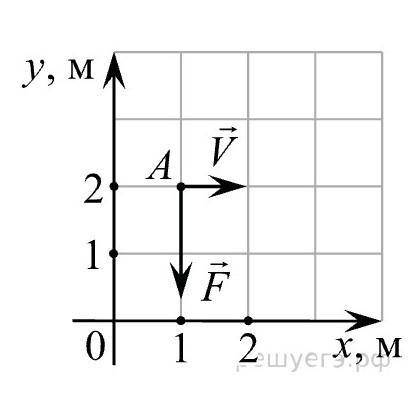
То­чеч­ное тело мас­сой 0,5 кг сво­бод­но дви­жет­ся по глад­кой го­ри­зон­таль­ной плос­ко­сти па­рал­лель­но оси Ox со ско­ро­стью V = 4 м/с В мо­мент вре­ме­ни t = 0, когда тело на­хо­ди­лось в точке A, на него на­чи­на­ет дей­ство­вать сила  мо­дуль ко­то­рой равен 1 Н. Чему равна ко­ор­ди­на­та этого тела по оси Оy в мо­мент вре­ме­ни t = 4 с?​

Итак, у нас есть точечное тело массой 0,5 кг, которое движется со скоростью V = 4 м/с по горизонтальной плоскости параллельно оси Ox. В момент времени t = 0 тело находится в точке A, на него начинает действовать сила модуль которой равен 1 Н. Мы хотим найти координату этого тела по оси Oy в момент времени t = 4 с.

Для решения этой задачи нам понадобятся формулы классической механики и некоторые принципы:

1. Закон инерции Галилея, который гласит, что тело продолжает двигаться прямолинейно и равномерно, пока на него не действует внешняя сила.
2. Второй закон Ньютона, который гласит, что сила, действующая на тело, равна произведению его массы на ускорение: F = m*a.
3. Закон сохранения энергии, который гласит, что сумма кинетической и потенциальной энергии тела остается постоянной, если на него не действуют внешние силы.

Теперь давайте решим задачу пошагово:

1. В момент времени t = 0 на тело начинает действовать сила F = 1 Н. Для нахождения ускорения, вызванного этой силой, используем второй закон Ньютона:

F = m*a
1 = 0,5*a
a = 2 м/с^2

Получили, что ускорение тела равно 2 м/с^2.

2. Так как тело движется со скоростью V = 4 м/с и на него действует постоянная сила, оно будет равномерно ускоренным.

3. Относительно оси Оy тело не испытывает никаких внешних сил, поэтому его координата по оси Оy остается постоянной.

4. Координату точки A по оси Оy можно найти с помощью формулы для равномерно ускоренного движения:

S = V*t + (1/2)*a*t^2,

где S - координата, V - начальная скорость, t - время, a - ускорение.

Так как тело движется по горизонтальной плоскости, начальная скорость по оси Оy равна нулю. Также учтем, что время t = 4 с, а ускорение a = 2 м/с^2.

S = 0 + (1/2)*2*(4^2)
S = 0 + (1/2)*2*16
S = 0 + 2*8
S = 16 м

Таким образом, координата точки A по оси Оy в момент времени t = 4 с равна 16 м.