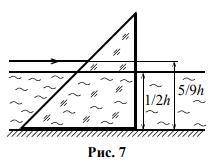
Стеклянную призму, основания которой представляют собой прямоугольные равнобедренные треугольники, поместили в широкий сосуд с водой, стоящий на столе, так уровень воды доходит до 1/2 высоты основания призмы. Луч падает на левую наклонную грань призмы горизонтально. Под каким углом к горизонтали луч выйдет из призмы, если входной луч попадает в призму на уровне 5/9 высоты основания призмы? Показатели преломления стекла и воды соответственно составляют n=1,5 nᵦ=1,35.
Другие вопросы по теме Физика
Популярные вопросы
- Кчетырём пристаням ежедневно причаливает 48 судов. сколько судов причаливает...
3 - 4,735: 0,5+14,95: 1,3+2,121: 0,7= 10 ,по действиям фотку лучше прислать...
3 - Впитомнике 50% фруктовых деревьев. 30% составляют груши.сколько груш...
3 - Перевести кезімнен естіген, үйренген,білген сөздерімнің ішінен бір...
2 - Объясни вычисления 567+9 439+5 356-7 564-9...
1 - Слова в разброс.составить предложение : england are private there schools...
2 - На какие две группы делятся гласные?...
1 - Прочитай текст найди и выпиши слова в которых все согласные мягкие...
2 - Велосипедист за 3часа проехал 54км.какое расстояние он проедет за следующие...
3 - Измени в уравнений одно число х-52=29; чтобы корень стал на 17 меньше;...
1
Объяснение:
Согласно закону Снелла:
n_1 sin〖φ_1 〗=n_2 sin〖φ_2 〗
n_1=1 - показатель преломления воздуха;
Луч падает на левую наклонную грань призмы под углом 450.
n_2=1,5 - показатель преломления стекла
n_3=1,35 - показатель преломления воды
sin〖φ_2 〗=(n_1 sin〖φ_1 〗)/n_2 =sin45/1,5=√2/3
φ_2=〖28〗^0
φ_2+φ_3=〖45〗^0
φ_3=〖45〗^0-〖28〗^0=〖17〗^0
n_2 sin〖φ_3 〗=n_3 sin〖φ_4 〗
sin〖φ_4 〗=(n_2 sin〖φ_3 〗)/n_3 =(1,5 sin17)/1,35=0,96
φ_4=〖73〗^0
φ_5=φ_6=φ_7=〖90-φ〗_4 〖=〖90〗^0-73〗^0=〖17〗^0
n_3 sin〖φ_7 〗=n_1 sin〖φ_8 〗
sin〖φ_8 〗=(n_3 sin〖φ_3 〗)/n_1 =(1,35 sin17)/1=0,39
φ_8=〖23〗^0
α=90-φ_8=〖67〗^0
ответ: 670 к горизонтали луч выйдет из призмы.