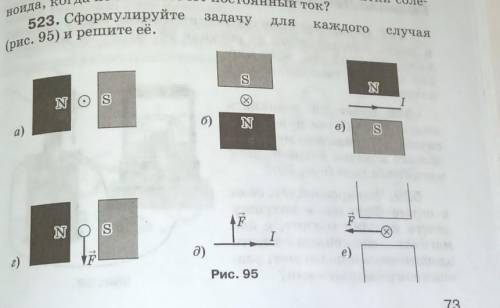
Сформулируйте задачу для каждого случая рис 95 и решите её
Другие вопросы по теме Физика
Популярные вопросы
- Найдите объем комнаты имеющей форму прямоугольного параллелепипеда если ее длина...
1 - Написать сочинение по языку. 50 ,...
2 - 20 ! ! в цилиндрической посуде (диаметр дна – 1,5 дм) уровень жидкости достигает...
1 - Назовите состав экспедиции ф.магеллана перед началом и в конце его экспедиции...
3 - Выписать слова,распределяя их по группам: проверяемая безударная гласная в корне...
3 - Круг разделён на три части двумя точками соотношениями 2: 5: 11 из маленького...
2 - Проанализировать какой из подходов более эффективный; содержательный или алфавитный...
2 - Таблиця форма держави/характерні риси...
1 - Построить круговую диаграмму вместимости сахара(г) на 100г фруктов: яблок-11,абрикос-10,банан-12,инжир-50,клубника-7...
2 - Дайте характеристику ломоносову или циолковскому 1. какие качества данной личности...
3
1. Прямоугольный треугольник A.
Задача: Найти длину гипотенузы треугольника A, если известны длины катетов a = 3 и b = 4.
Решение:
Используем теорему Пифагора, согласно которой квадрат гипотенузы треугольника равен сумме квадратов катетов.
a^2 + b^2 = c^2
3^2 + 4^2 = c^2
9 + 16 = c^2
25 = c^2
Извлекаем корень: c = √25
Таким образом, длина гипотенузы треугольника A равна 5.
2. Прямоугольный треугольник B.
Задача: Найти длину катета b треугольника B, если известна длина гипотенузы c = 10 и катета a = 6.
Решение:
Снова используем теорему Пифагора.
a^2 + b^2 = c^2
6^2 + b^2 = 10^2
36 + b^2 = 100
b^2 = 100 - 36
b^2 = 64
Извлекаем корень: b = √64
Таким образом, длина катета b треугольника B равна 8.
3. Прямоугольный треугольник C.
Задача: Найти площадь треугольника C, если известны длины катетов a = 5 и b = 12.
Решение:
Площадь прямоугольного треугольника можно найти, используя формулу A = (a * b) / 2, где A - площадь, a и b - длины катетов.
A = (5 * 12) / 2
A = 60 / 2
A = 30
Таким образом, площадь треугольника C равна 30.