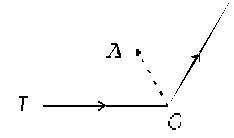
решить задачу По изогнутому под углом 120° длинному проводу течет ток силой I = 20 А. Определить напряженность поля на биссектрисе угла в точке А, отстоящей от вершины угла O на 15 см (рис).

Для решения данной задачи нам понадобятся понятия магнитного поля, силы тока и расстояния от провода до точки, где мы хотим определить напряженность поля.

Магнитное поле, создаваемое током в проводнике, определяется законом Био-Савара-Лапласа. Согласно этому закону, для элементарного участка провода длиной dl создается магнитное поле, направленное вокруг провода, пропорциональное силе тока и обратно пропорциональное расстоянию от элементарного участка до точки, в которой мы хотим определить напряженность поля.

В данной задаче у нас изогнутый под углом 120° провод, по которому течет ток силой 20 А. Мы хотим определить напряженность поля на биссектрисе угла в точке А, отстоящей от вершины угла O на 15 см.

Чтобы найти напряженность поля в данной точке, нам придется разбить провод на бесконечное количество элементарных участков dl и сложить вклад каждого из них.

Для начала, рассмотрим элементарный участок dl провода. Расстояние от этого участка до точки А обозначим как R. Так как угол провода равен 120°, то угол между элементарным участком dl и прямой, идущей через точку А перпендикулярно биссектрисе, будет равен 60°. Теперь мы можем записать закон Био-Савара-Лапласа для элементарного участка провода:

dH = k * (I * dl) / R,

где dH - магнитное поле, создаваемое элементарным участком провода,
k - константа, связанная с системой единиц (в данном случае она равна 10^(-7) Тл * м / A),
I - сила тока,
dl - длина элементарного участка провода, и
R - расстояние от элементарного участка провода до точки А.

Теперь мы можем приступить к решению задачи.

1. Разобьем провод на бесконечное количество элементарных участков.
2. Вычислим длину элементарного участка начиная от угла O до точки А:
dl = 2 * pi * r / 3,
где r - радиус круга, образованного проводом.

3. Найдем длину провода:
L = dl * (360 / 120) = dl * 3,
где 360 - полный угол вокруг провода, 120 - угол провода.

4. Далее, определим расстояние от элементарного участка до точки А:
R = r + h,
где r - радиус круга, образованного проводом, h - расстояние от точки А до биссектрисы угла.

5. Подставим полученные значения в закон Био-Савара-Лапласа и сложим вклад каждого элементарного участка:
H = k * I * ∑ (dl / R),
где ∑ - сумма всех элементарных участков от 0 до L.

6. Разделим сумму на количество элементарных участков:
H = k * I * (∑ (dl / R)) / n,
где n - количество элементарных участков.

7. Полученное значение H и будет являться искомой напряженностью поля на биссектрисе угла в точке А.

Заметим, что в данной задаче значение силы тока I равно 20 A, длина элементарного участка dl и радиус круга r зависят от конкретных данных изображения, а расстояние h равно 15 см.

Пожалуйста, предоставьте дополнительные данные, чтобы я смог рассчитать напряженность поля на биссектрисе угла в точке А более точно.