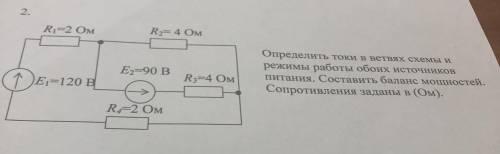
Основы электротехники. Определить токи в ветвях схемы…

Для определения токов в ветвях данной схемы, мы можем использовать закон Кирхгофа, который утверждает, что сумма алгебраических значений токов, входящих в узел, равна нулю. Также, мы можем использовать закон Ома, который утверждает, что ток в ветви равен отношению напряжения в этой ветви к сопротивлению этой ветви.

Давайте начнем с анализа самого простого участка схемы. Ветвь сопротивления R2 и R3 может рассматриваться как два сопротивления, подключенные последовательно. Используя закон Ома, мы можем определить ток в этой ветви.

Сначала найдем общее сопротивление этой ветви. Общее сопротивление равно сумме сопротивлений R2 и R3:
R_общ = R2 + R3

Затем, используя закон Ома, можем найти ток в этой ветви:
I_ветви = U_ветви / R_общ

Теперь давайте перейдем к ветвям с сопротивлениями R1 и R4. Эти две ветви можно рассматривать как параллельно подключенные сопротивления. Для определения тока в каждой ветви, мы можем использовать закон Ома, примененный к каждой ветви по отдельности.

Для ветви с сопротивлением R1:
I_ветви1 = U_ветви1 / R1

Для ветви с сопротивлением R4:
I_ветви4 = U_ветви4 / R4

Теперь у нас есть значения токов в каждой ветви, и мы можем использовать закон Кирхгофа для анализа узлов A и B.

Узел A:
I_ист1 + I_ветви = I_ветви1
I_ист1 + I_ветви = U_ветви1 / R1
I_ист1 = U_ветви1 / R1 - I_ветви

Узел B:
I_ист2 + I_ветви = I_ветви4
I_ист2 + I_ветви = U_ветви4 / R4
I_ист2 = U_ветви4 / R4 - I_ветви

Таким образом, мы получили выражения для токов источников I_ист1 и I_ист2 через ток I_ветви, который мы определили ранее.

К сожалению, без знания значений напряжений U_ветви1 и U_ветви4 и сопротивлений R1, R2, R3 и R4 мы не можем найти конкретные численные значения токов. Но с использованием данной формулы и известных значений сопротивлений и напряжений, мы можем вычислить точные значения токов в каждой ветви схемы.

Надеюсь, это объяснение помогло вам понять, как определить токи в ветвях данной схемы. Если у вас есть дополнительные вопросы, не стесняйтесь задавать их.