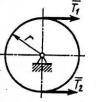
Определить угловое ускорение диска массой m = 50 кг, радиуса r = 0,3 м, если натяжение ведущей и ведомой ветвей ремня соответственно равны Т1 = 2Т2 = 100 Н. Радиус инерции
диска относительно оси вращения iz = 0,2 м
Другие вопросы по теме Физика
Популярные вопросы
- Жабық есік саясаты дегеніміз не??...
3 - 94÷26 решите випробовування...
1 - За 3,5 м ткани заплатили 619,5 р. Вычисли стоимость 11,25 м этой...
3 - Які слова можна використати для характеристики дроворуба?...
1 - С ДАНО,РЕШЕНИЕМ И ОТВЕТОМ,ЗАРАНЕЕ У человека ген карих глаз (А)...
3 - Яйцеклітина формується одна, а сперматозоїдів багато, чому?...
1 - Составьте или выпишите из худ произведений 4 предложения с прямой...
3 - У битві біля міста Липани в 1434р. зазнали поразки. а) часники.в)хрестоносці....
2 - ещё два слова которых нет на картинке stürmischsonning...
1 - У повітрі залізна деталь розтягнула пружину динамометра з силою...
1
1. Начнем с выражения момента силы, действующей на диск:
М = I * α,
где М - момент силы, α - угловое ускорение диска, I - момент инерции диска относительно оси вращения.
2. Найдем момент инерции диска:
I = m * r^2,
где m - масса диска, r - радиус диска.
3. Подставим значение радиуса инерции:
I = 50 кг * (0,3 м)^2 = 4,5 кг * м^2.
4. Теперь найдем разность натяжений в ремне:
ΔТ = Т1 - Т2 = 100 Н - 100 Н = 0.
5. Зная, что натяжение в ремне связано с моментом силы, можно записать:
М = ΔТ * r.
6. Подставим значения и получим:
0 = 0 * r.
7. Таким образом, момент силы равен нулю.
8. Возвращаемся к первому уравнению и подставляем полученное значение момента силы:
0 = I * α.
9. Разделим обе части уравнения на I:
0 = α.
10. Получили, что угловое ускорение диска равно нулю.
Ответ: Угловое ускорение диска равно нулю.