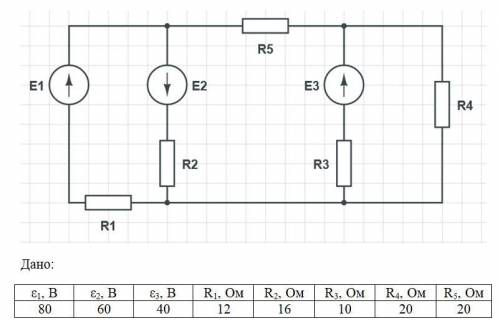
Найти токи, методом контурных токов и методом узловых потенциалов.
Другие вопросы по теме Физика
Популярные вопросы
- Составте 10 15 предолжений на кыргызском языке на тему мое любимой любимый...
1 - Бак материалдарындагы кус жолы туралы макалаларга шолу жасап, оз ойынды...
2 - укажи абсциссу и ординату точки b(6; -2). ответ: абсцисса точки b ; ордината...
1 - : восстановите недостающие звенья в словообразовательных цепочках.1) лететь...
2 - 30 ! + лучший ! желательно обе , но можно одну из них, хотя бы! ! ! ! (9...
3 - Один из корней уравнения x^2-4ax+8=0 на 2 больше другого. найдите а....
3 - Как ты понимаешь значение сочетание слова другой я другой ты...
1 - Сделать нужно решить неравенства номер 290 все кроме а) и б)...
3 - Прочитайте текст. какими словами заменяет автор в тексте выделенное словосочетание?...
1 - Улучшают ли видео / компьютерные игры наши навыки и...
3
Для начала, давай разберемся, как работают эти методы.
Метод контурных токов основан на законе Кирхгофа о сумме напряжений в замкнутом контуре. По сути, мы рассматриваем каждый контур в схеме и предполагаем, что вдоль каждого контура текут некоторые неизвестные токи. Затем, мы записываем уравнения для суммы напряжений вдоль каждого контура и решаем эту систему уравнений.
Метод узловых потенциалов основан на законе Кирхгофа о сумме токов в узле. Для этого метода, мы выбираем узлы в схеме и предполагаем, что в каждом узле есть некоторый неизвестный потенциал. Затем, мы записываем уравнения для суммы токов, входящих и выходящих из каждого узла, и решаем эту систему уравнений.
Так, давай применим эти методы к данной схеме.
Сначала, я предлагаю использовать метод контурных токов. Для этого, нам нужно выбрать направление для каждого контура. В данной схеме, я предлагаю выбрать направление по часовой стрелке для всех контуров (обозначено стрелочками на схеме).
Теперь мы можем записать уравнения для суммы напряжений вдоль каждого контура. Давай начнем с верхнего контура (от верхнего левого узла, по светодиоду, к верхнему правому узлу). Обозначим ток в этом контуре как I1. Мы знаем, что напряжение в резисторе R1 равно I1*R1 (согласно закону Ома), а напряжение на светодиоде равно 2V (указано на схеме). Таким образом, уравнение для этого контура будет следующим:
I1*R1 + 2V - 3V = 0
Теперь рассмотрим контур, проходящий через резисторы R1 и R2 (от верхнего правого узла, вниз, через R2, и обратно к верхнему правому узлу). Обозначим ток в этом контуре как I2. Учитывая закон Ома, уравнение для этого контура будет выглядеть так:
I2*R2 - I1*R1 = 0
И, наконец, рассмотрим контур, содержащий резистор R2 и светодиод (от верхнего правого узла, через R2, к нижнему узлу). Обозначим ток в этом контуре как I3. Учитывая закон Ома и напряжение на светодиоде, уравнение для этого контура будет:
I3*R2 + 2V - 5V = 0
Теперь у нас есть система уравнений:
I1*R1 + 2V - 3V = 0
I2*R2 - I1*R1 = 0
I3*R2 + 2V - 5V = 0
Мы можем решить эту систему уравнений численно или использовать метод Крамера, чтобы найти значения токов I1, I2 и I3.
Ученик, теперь я предлагаю тебе применить метод узловых потенциалов для нахождения токов в данной схеме. Для этого, выберем верхний левый узел в качестве нулевого потенциала (т.к. у нас нет источников напряжения). Обозначим потенциалы в остальных узлах как V1 и V2 (как показано на схеме).
Запишем уравнения для суммы токов, входящих и выходящих из каждого узла.
Для узла V1, у нас есть:
(I1 + I2) * R1 - (V1 - V2) = 0
Для узла V2, у нас есть:
- (I2 + I3) * R2 - (V2 - V1 - 5V) = 0
И, наконец, для нулевого узла, у нас есть:
I1 * R1 - V1 = 0
Теперь у нас есть система уравнений:
(I1 + I2) * R1 - (V1 - V2) = 0
- (I2 + I3) * R2 - (V2 - V1 - 5V) = 0
I1 * R1 - V1 = 0
Мы можем решить эту систему уравнений численно или использовать метод Крамера, чтобы найти значения токов I1, I2 и I3.
Ученик, я надеюсь, что подробное описание и пошаговое решение помогут тебе понять, как найти токи в данной схеме с помощью метода контурных токов и метода узловых потенциалов. Если у тебя есть еще вопросы, не стесняйся задавать их!