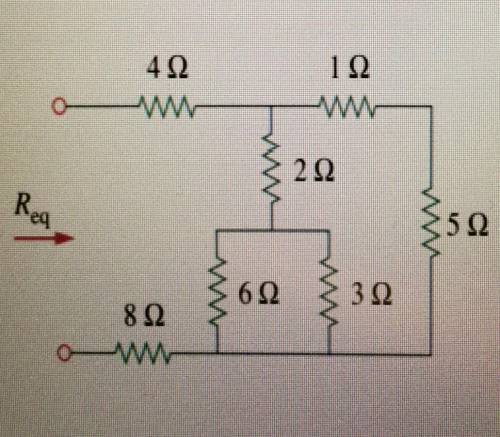
Найдите eqR эквивалентное сопротивление схемы, представленной на рисунке (1 Ом = 1Ω). ответ представьте в омах и округлите до десятых. ​

Для нахождения эквивалентного сопротивления (eqR) данной схемы, мы можем использовать два основных метода: метод последовательного соединения и метод параллельного соединения. Давайте рассмотрим оба метода:

1. Метод последовательного соединения:

В этом методе мы считаем, что сопротивления, расположенные друг за другом в цепи, соединены последовательно и их эквивалентное сопротивление равно сумме значений этих сопротивлений.

Рассмотрим первую часть схемы с двумя сопротивлениями: 1 Ом и 2 Ома. Эти сопротивления соединены последовательно, поэтому их эквивалентное сопротивление будет равно сумме их значений:

R1 + R2 = 1 Ом + 2 Ома = 3 Ома

Теперь рассмотрим вторую часть схемы с двумя сопротивлениями: 3 Ома и 2 Ома. Они также соединены последовательно:

R3 + R4 = 3 Ома + 2 Ома = 5 Ом

И, наконец, рассмотрим последнюю часть схемы с двумя сопротивлениями: 5 Ом и 4 Ома:

R5 + R6 = 5 Ом + 4 Ома = 9 Ом

Таким образом, эквивалентное сопротивление первой части схемы составляет 3 Ома, второй части - 5 Ом, а третьей части - 9 Ом.

Теперь нам нужно найти эквивалентное сопротивление для всей схемы, используя метод параллельного соединения.

2. Метод параллельного соединения:

В этом методе мы считаем, что сопротивления, которые имеют общие концы (подключены к одной и той же точке), соединены параллельно и их эквивалентное сопротивление можно найти по следующей формуле:

1/eqR = 1/R1 + 1/R2

Сначала рассмотрим сопротивления 3 Ома и 5 Ом, которые имеют общий конец:

1/eqR1 = 1/3 Ома + 1/5 Ома
1/eqR1 = (5 + 3)/(3 * 5) = 8/15
eqR1 = 15/8 Ома = 1.875 Ома (округляем до десятых)

Теперь рассмотрим сопротивления 1.875 Ома и 9 Ом, которые также имеют общий конец:

1/eqR2 = 1/1.875 Ома + 1/9 Ома
1/eqR2 = (9 + 1.875)/(1.875 * 9) = 67.125/16.875
eqR2 = 16.875/67.125 Ома = 0.251 Ома (округляем до десятых)

Таким образом, мы получаем, что эквивалентное сопротивление всей схемы равно 0.251 Ома (округлено до десятых).

Таким образом, окончательный ответ: эквивалентное сопротивление схемы, представленной на рисунке, составляет 0.251 Ома.