На границе раздела двух несмешивающихся жидкостей, имеющих плотности ρ1 = 600 кг/м3 и ρ2 = 4ρ1 плавает шарик (см. рисунок). Какова должна быть плотность шарика ρ, чтобы выше границы раздела жидкостей была одна четверть его объёма? Решение этой задачи необходимо записатьна отдельном листе, подписать, сфотографировать и прикрепить в данном тесте.
Другие вопросы по теме Физика
Популярные вопросы
- Тəтті қиял Ғарыш əлемі. Кішкентай ғарышкер ғарыш əлеміне саяхаттады....
1 - Құлагер фильмiне барлық бөлiмге жоспар құру...
3 - Отметь Приключения Герды в сказке Снежная королева Верных ответов:2Была...
1 - решить желательно на листочке...
1 - Добери до поданих слів синоніми з НЕ і запиши їх за зразком:ЗРАЗОК...
3 - Если деталь симметрична вертикально, то делать разрез без обозначений...
3 - тапкан археолог 2.зерттеген уакыт МНЕ СЕЙЧАС НАДО ЗДАТЬ БЫСТРЕЕ...
2 - Як в домашніх умовах можна довести наявність явища інерції тіл?...
2 - 2(x-1,5) +5 — 2 және 1,2 – 2а — т+4 теңдеулері а параметрінің қандай...
3 - Написать требования безопасности при проведении занятий на улице...
3
Введение и выражение величин:
Пусть плотность первой жидкости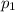 , второй жидкости
, второй жидкости 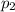 , а шара
, а шара 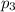 , тогда запишем общий объём шара
, тогда запишем общий объём шара 
Найдем объем шара находящийся над водой, для этого общий объем разделим на 4 (по условию), и получим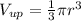 (1)
(1)
Повторим для нижней части шара, только умножим на 3/4, так как логично, что оставшаяся часть шара под разделом жидкостей, и получим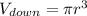 (2)
(2)
Чтобы найти массы этих частей шара, надо найденный объем умножить на плотность шара:
Работа с формулами и уравнением:
На шар действуют 2 силы: Архимеда и тяжести, так как шар неподвижен, то сила действующая на обе части "вниз", равна силе действующей на обе части "вверх", запишем общий вид:
Подставим объем и массы из пунктов (1-4) и сократим на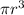 и на
и на 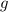 , в итоге останется:
, в итоге останется:
Подставим значения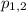 и решим уравнение:
и решим уравнение:
Получим те самые циферки из ответа